Как открывали закон всемирного тяготения

Как открывали закон всемирного тяготения

Вы, конечно, знаете, что вес — это просто сила, с которой Земля притягивает к себе разные предметы. Одно и то же тело на Земле и на Луне весит по-разному, хотя масса его не меняется. Величина силы тяжести зависит от массы не только притягиваемого тела, но и притягивающего, а также от расстояния между их центрами. Вот только как зависит? От успеха решения этой задачи в XVII веке зависело буквально все развитие дальнейшей науки. Ученые это хорошо понимали и напрягали усилия, чтобы вывести закон, который связывал силу тяготения и массы тел.

В то время Исаак Ньютон упорно изучал движение Луны, задавая себе вопрос: «Что удерживает Луну от падения на Землю и какая сила движет ею по орбите вокруг Земли?» Эти вопросы тогда занимали не одного его. Едва ли не все ученое общество Лондона размышляло на ту же тему. Однажды астроном Галлей, друг и почитатель Ньютона, встретился в лондонском кафе с архитектором Реном. Оба сразу же заговорили о злободневных научных вопросах. К ним подошел Гук-наблюдатель и демонстратор опытов в Лондонском королевском обществе. Оказалось, что все трое немало времени и сил отдали доказательству того, что под действием силы тяжести, которая убывает пропорционально квадрату расстояний, движение небесных тел должно совершаться по кеплеровским эллиптическим орбитам, а не по кругам, как считалось раньше. Но доказательство ни у кого не получилось.

Следует заметить, что эта идея уже давно витала в воздухе. О ней говорили и даже писали. Оставалось ее только доказать математически. Жил в то время один малоизвестный сегодня итальянский натуралист по имени Джиованни Борелли. Занимаясь изучением движения спутников Юпитера, открытых Галилеем, он пришел к интересному заключению. «Движение небесных тел определяется взаимодействием двух сил, — говорил он. — Одной, направленной к центру вращения, и другой — от центра». Борелли рассуждал: предположим, что планета находится на таком расстоянии от Солнца и движется с такой скоростью, что стремление от центра меньше силы притяжения. Тогда планета будет приближаться к светилу по спирали, пока обе силы не уравновесятся. Предположим дальше, что по инерции, открытой Галилеем, планета проскочила нейтральную орбиту и приблизилась к Солнцу ближе положенного. Тогда сохранившаяся скорость движения заставит центробежную силу преодолеть притяжение и планета станет удаляться от светила.

Об этих рассуждениях Борелли знали многие. Но в них не было ни строчки неопровержимых математических доказательств. Итальянский ученый просто предполагал существование силы притяжения и из нее логически выводил необходимость обращения планет по орбитам.

Рен, самый богатый из всех троих джентльменов, сошедшихся в кафе, чисто в английском вкусе предложил на пари выплатить премию тому, кто первым решит задачу. Галлей и Гук согласились.

Прошло некоторое время, и Галлей как-то зашей к Ньютону по делам. Он рассказал ему о споре и о пари. Каково же было его удивление, когда его ученый друг с жаром заявил, что не только сам давно занимается тою же проблемой, но и почти имеет готовое решение.

Ньютон действительно давно рассуждал о причинах, удерживающих Луну на своей орбите. Искал силы, заставляющие наш спутник обращаться вокруг Земли. Упорно думал, пока ему не открылась вдруг простая истина. Да ведь для такого движения никакой дополнительной силы, кроме притяжения, и не нужно! Помните закон, гласящий, что ежели на тело не действует никакая посторонняя сила, то оно летит себе прямо с постоянной скоростью. Не так ли движется и Луна? Она летит себе прямолинейно в пространстве, а притяжение Земли ее все время заворачивает. И Луна падает, падает на Землю, но никак не может упасть…

Для окончательного вывода Ньютону нужны были точные сведения об орбите Луны и периоде ее обращения. Он попросил представить их ему королевского астронома Флемстида. Но тот, верный своему пренеприятному характеру, заявил в ответ, что не намерен потакать причудам мистера Ньютона. Пришлось Галлею чуть ли не похитить у королевского астронома результаты его наблюдений, чтобы передать их Ньютону. И тогда, менее чем через месяц, тот отослал своему другу готовую рукопись краткого мемуара с полным решением спорной задачи.

Ньютон просил пока не публиковать его сообщения, но зарегистрировать его в королевском обществе на случай споров о приоритете. Спустя год эта работа увидела свет.

«Мистер Ньютон разработал руду, которую я накопал», — не без сарказма заметил Флемстид.

«Если он накопал руду, то я смастерил из нее золотое кольцо», — парировал Ньютон, который хоть и не любил споров, но и в долгу не оставался, когда о его работе отзывались без должного уважения.

Конечно, одной теории Луны было недостаточно для утверждения о всеобщности закона всемирного тяготения. Но вслед за расчетами лунного движения последовали расчеты движения и многих других небесных тел, и замечательное уравнение Ньютона обрело статус всемирного закона.

Вы, наверное, помните его формулу 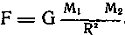, где F — сила притяжения, M₁ и М₂ — массы притягивающихся тел, R — расстояние между ними, a G — гравитационная постоянная, или коэффициент пропорциональности в законе тяготения, который еще предстояло определять.

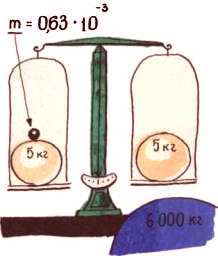
Пользуясь созданной теорией, Ньютон сумел определить отношения масс небесных тел. Например, отношение массы Земли к массе Солнца, массы Юпитера к массе Солнца. Но вычислить массу каждого тела по отдельности никак не удавалось. Для этого нужно было точно знать коэффициент пропорциональности, то есть гравитационную постоянную. А для ее определения следовало поставить очень тонкие опыты по измерению притяжения двух тел с известными массами.