2. Теотиуакан — Мемфис — Санкт-Петербург

2. Теотиуакан — Мемфис — Санкт-Петербург

Уже говорилось, что в день зимнего солнцестояния южные грани великих египетских пирамид оказываются перпендикулярными плоскости, в которой движутся планеты, и солнечные лучи падают на них строго под прямым углом (рис. 9). Если на поверхности этих граней разместить солнечные батареи, то в самый короткий в Северном полушарии планеты день в году условия для поглощения солнечного излучения будут наилучшими.

Понятно, что те же пирамиды не могли бы выполнять функцию идеальных аккумуляторов энергии в точках Земли с отличающимися географическими координатами, ибо со сменой широты изменялся бы угол наклона граней по отношению к плоскости Эклиптики. Например, на экваторе, где широта равна 0°0?, угол наклона грани пирамиды, построенной для выполнения функций «абсолютного» поглотителя солнечного излучения, должна была бы равняться точно углу склонения экватора от Эклиптики, то есть 23°27?. Каждой широте планеты соответствует своя особенная геометрия «идеальной» пирамиды.

Чтобы проверить эту теорию, попытаемся сравнить пирамиды одинаковой высоты, но построенные на разных широтах, разных континентах, разными народами. Существуют два равновеликих сооружения, построенные независимо в разных концах мира. В городе-святилище народа Майя Теотиуакан рядом с современным Мехико есть пирамида, которую называют пирамидой Солнца. Ее высота — 65 м. Наименьшая из пирамид Мемфисского некрополя — пирамида Микерина (Менкаура) — сегодня возвышается над песком на 62–63 м.

Изначально она имела высоту 65,6 м. То есть «образцы» для исследования выбраны идеально.

Сравним пирамиды.

Угол наклона граней усыпальницы Микерина (Менкаура) — 53°07?28?. Для Мексики в точке с координатой 19°20? северной широты расчетный угол наклона плоскостей сооружения, в соответствии со сформулированной теорией, должен быть 42°47?, так как:

19°20? + 23°27? = 42°47?.

Фактический угол наклона боковых граней пирамиды Солнца в Теотиуакане — чуть больше 43°. Правильнее говорить лишь о среднем угле наклона, ибо пирамида Солнца ступенчатая и ее геометрические характеристики варьируются по высоте. Разница между 53°07?28? и 43° (расчетными 42°47?) точно соответствует разнице широт Египта и Мексики. Теория подтверждается.

Одновременно с подтверждением наших предположений мы доказали удивительный факт. Плоскости южных граней двух реально существующих древних сооружений, воздвигнутых в удаленных друг от друга на треть окружности Земли точках — грани пирамид Солнца в Теотиуакане и Мике-рина (Менкаура) в Египте… параллельны! И параллельны они ни в какой-то определенный день года, а всегда!

Подтвердим этот важнейший вывод еще раз. Каким бы был угол наклона плоскости южной грани пирамиды Микерина (Менкаура) по отношению к земной поверхности, если бы вдруг, по нашей воле, могущественный джин перенес этот грандиозный кристалл из Мемфиса (29°58?51? северной широты) в точку с координатами 19°20? северной широты, не меняя пространственно расположения самой плоскости? Это нетрудно вычислить, ибо плоская поверхность сохраняет свою ориентацию, а площадка-основание под пирамидой как бы медленно поворачивается по мере перемещения к югу:

53°07?28? ? (29°58?51? ? 19°20?) = 42°28?37?.

Угол наклона боковых граней пирамиды Солнца в Теотиуакане — чуть больше 43°. Некоторое, очень малое несоответствие связано с тем, что в расчетах использована широта Мехико, а не Теотиуакана и нам не известно точное значение угла наклона граней мезоамериканской пирамиды. Кроме того, святилища доколумбовой Америки могут быть старше африканских. Расхождение в один полный градус может быть объяснено смещением оси Земли на градус. Подобное угловое смещение оси планеты может произойти не меньше чем за 17 000 лет. Есть о чем подумать.

После подтверждения нашей теории интересно узнать, какая широта на поверхности Земли «превращает» угол наклона пирамиды в предельный угол — в 90°, при котором противоположные грани правильно спроектированного многогранника станут параллельными и перестанут где-либо в пространстве пересекаться? Если бы в городах Александрия, Константинополь, Киев, Санкт-Петербург и севернее строились пирамиды, то по мере продвижения к Северному полюсу они должны были бы становиться все выше и выше, а их четыре треугольные грани все расходились бы и расходились, как лепестки цветка. Сказанное иллюстрируется информацией, почерпнутой из источника [46]: «При архитектурных обмерах Парфенона (Афины, 447–438 годы до н. э., архитекторы Иктин и Калликрат) исследователи обнаружили, что в постройке, как и в человеческом теле, нет ни прямых линий, ни ровных плоскостей: все линии слегка изогнуты, плоскости чуть выпуклы или вогнуты, оси колонн, при мысленном их продолжении вверх, пересекаются (!) в одной точке…»

То есть Парфенон — своеобразная пирамида с большим, чем у египетских пирамид, углом наклона граней к основанию.

Но перейдем к тому, что нас более всего интересует.

Для широты Санкт-Петербурга расчетный угол наклона граней пирамиды равен 83°22?, ибо:

59°55? + 23°27? = 83°22?.

На отметке 60° северной широты угол наклона будет 83°27?. Если строить на берегу Невы пирамиду, точно выполняя все предписания древних египтян, то сооружение оказалось бы вытянутым, чуть ли не как… шпиль колокольни Петропавловского собора.

Попробуем вывести формулу для вычисления величины угла между гранями у вершины пирамиды, воздвигаемой на параллели Y° северной широты:

180° ? 2 ? (Y° + 23°27?) = 133°06? ? 2 ? Y°.

Если угол у основания пирамиды Y° равен 59°55? — 60°, то угол у вершины окажется равным 13°06? — 13°10?.

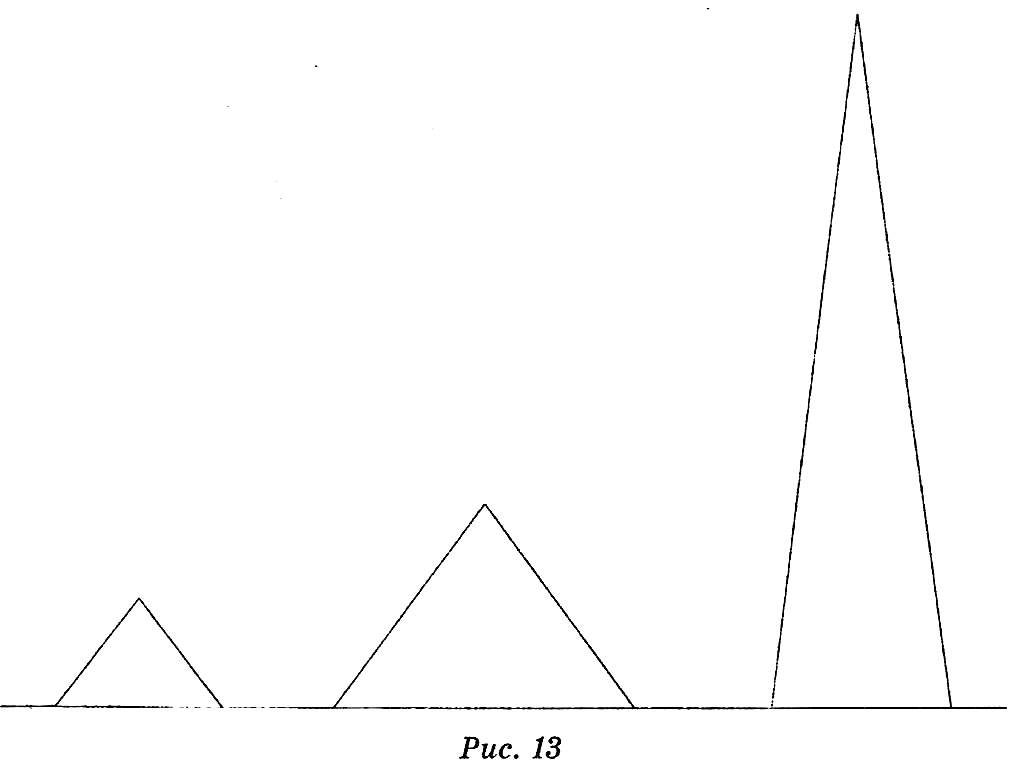
На рис. 13 сопоставлены пирамида Хеопса (Хуфу), Великая Незримая пирамида (ее надпесочная часть) и пирамида широты Санкт-Петербурга (с основанием, идентичным пирамиде Хеопса). Конечно, говорить о изяществе композиции не приходится. Но талантливому архитектору достаточно поставить маленькую точку-кляксу где-нибудь на поверхность грани пирамиды, и она оживет, начнет радовать глаз. Ну а что нас ждет севернее Санкт-Петербурга?

Широту точки, где грани пирамиды становятся параллельными друг другу, определяем элементарным вычитанием:

90°00? ? 23°27? = 66°33?.

66°33? северной широты — это координата линии, которую географы называют Северным полярным кругом. На этой широте Солнце видно не намного поднявшимся или наполовину зашедшим за горизонт. Его лучи скользят параллельно земной поверхности, и поймать их можно, только поставив вертикальную стену. Отсюда расчетный наклон граней пирамиды — 90°00? (прямой угол). Число 66°33? (широта Северного полярного круга) позволяет:

а) по-новому взглянуть на содержание таблиц 3 и 4:

66°33? / 7 = 9°30?26?,

66°33? ? 3 = 199°39?,

200° ? 199°39? = 21?;

б) сделать более осмысленной формулу для вычисленияугла у вершины оптимальной (в описанном ранее смысле)пирамиды, воздвигаемой на широте Y°:

угол между гранями у вершины = 2 ? (66°33? ? Y°);

в) уточнить некоторые наши представления о пространстве-времени структуры (Су)Меру.

Гора (Су)Меру устремляется к самой высшей точке мироздания, какую могут себе представить жрецы, возводящие ее в своем воображении. На Земле — одной из планет Солнечной системы — такой точкой может быть только какое-то особенное место поверхности земного шара, ибо межпланетное пространство неосязаемо. И тут мы, получив последние результаты, вдруг понимаем, что, как бы ни поворачивалась при движении вокруг Солнца и при вращении вокруг собственной оси наша планета, одна из точек Северного полярного круга обязательно всегда находится выше всей планеты, если за нулевую плоскость брать плоскость, в которой движется Земля, — плоскость Эклиптики. Эту точку — точку «X» — на рис. 9 можно уверенно назвать вершиной мира. Истинной вершиной мира является не Северный полюс, а точка на Северном полярном круге, отстоящая от полюса на 23°27? северной широты.