3. Принцип затухания частот Метод упорядочивания исторических текстов во времени

3. Принцип затухания частот

Метод упорядочивания исторических текстов во времени

Принцип затухания частот и основанный на нем метод предложен и разработан мною в [884], [886], [888], [1129], [891], [895], [898], [901], [1130].

Настоящий метод позволяет находить хронологически правильный порядок отдельных фрагментов текста, обнаруживать в нем дубликаты на основе анализа, например, совокупности собственных имен, упомянутых в тексте. Как и в предыдущих методиках, мы стремимся к созданию метода датировки, основанного на численных, количественных характеристиках текстов и не обязательно требующего анализа смыслового содержания текстов, которое может быть весьма многозначно и расплывчато.

Если в документе упомянуты какие-либо «знаменитые», ранее известные нам персонажи, описанные в других, уже датированных хрониках, то это позволяет датировать описанные в тексте события. Однако если такое отождествление сразу не удается и если, кроме того, описаны события нескольких поколений с большим количеством ранее неизвестных действующих лиц, то задача установления тождества персонажей с ранее известными усложняется. Для краткости назовем фрагмент текста, описывающий события одного поколения, «главой-поколением».

Будем считать, что средняя длительность одного «поколения» — это средняя длительность правления реальных царей, зафиксированных в дошедших до нас летописях. Эта средняя длительность правления царей вычислена автором настоящей книги при обработке хронологических таблиц Блера [76]. Она оказалась равной 17,1 года [884].

При работе с реальными историческими текстами выделение в них «глав-поколений» иногда наталкивается на трудности. В таких случаях мы ограничивались лишь приблизительным разбиением текста на последовательные фрагменты. Пусть летопись X описывает события на достаточно большом интервале времени (А, В), на протяжении которого сменилось, по крайней мере, несколько поколений персонажей. Пусть летопись X разбита на «главы-поколения» X(T), где T — порядковый номер поколения, описанного во фрагменте X(T) в той нумерации «глав», которая фиксирована в тексте.

Возникает вопрос: правильно ли занумерованы, упорядочены эти «главы-поколения» в летописи? Или же, если эта нумерация утрачена или сомнительна, то как ее восстановить? Другими словами, как правильно расположить во времени «главы» друг относительно друга? Оказывается, для реальных исторических текстов в подавляющем большинстве случаев выполняется следующая «формула»-правило: полное имя = персонаж. Это означает следующее.

Пусть интервал времени, описываемый летописцем, достаточно велик, например, составляет несколько десятков или сотен лет. Тогда, — как было проверено нами в результате анализа большого набора исторических документов, — в подавляющем большинстве случаев РАЗНЫЕ ПЕРСОНАЖИ имеют в одном и том же тексте РАЗНЫЕ ПОЛНЫЕ ИМЕНА. Полное имя может состоять из нескольких слов, например, Карл Плешивый. Другими слова ми, ЧИСЛО РАЗНЫХ ЛИЦ С ОДИНАКОВЫМИ ПОЛНЫМИ ИМЕНАМИ НИЧТОЖНО МАЛ? ПО СРАВНЕНИЮ С КОЛИЧЕСТВОМ ВСЕХ ПЕРСОНАЖЕЙ. Это верно для всех нескольких сотен исследованных нами исторических текстов, описывающих Рим, Грецию, Германию, Италию, Россию, Англию и т. д. Ничего удивительного в этом нет. В самом деле, летописец заинтересован в различении разных персонажей, чтобы избежать путаницы. Простейший способ добиться этого — присвоить разным лицам разные полные имена. Это простое психологическое обстоятельство и подтверждается подсчетами.

Сформулируем теперь ПРИНЦИП ЗАТУХАНИЯ ЧАСТОТ, описывающий хронологически правильный порядок «глав-поколений».

При правильной нумерации «глав-поколений» летописец, ПЕРЕХОДЯ ОТ ОПИСАНИЯ ОДНОГО ПОКОЛЕНИЯ К СЛЕДУЮЩЕМУ, СМЕНЯЕТ И ПЕРСОНАЖЕЙ. А именно, при описании поколений, предшествующих поколению с номером Q, он ничего не говорит о персонажах этого поколения, так как они еще не родились. Затем, при описании поколения Q, летописец именно здесь больше всего говорит о персонажах этого поколения, поскольку с ними напрямую связаны описываемые им события. Наконец, переходя к описанию последующих поколений, летописец все реже и реже упоминает о прежних персонажах, так как описывает новые события, персонажи которых вытесняют умерших.

Здесь важно подчеркнуть, что мы имеем в виду не какие-то отдельные имена, а полный резервуар всех имен, использовавшихся в поколении с номером Q.

Вкратце наша модель формулируется так. КАЖДОЕ ПОКОЛЕНИЕ РОЖДАЕТ НОВЫЕ ИСТОРИЧЕСКИЕ ЛИЦА. ПРИ СМЕНЕ ПОКОЛЕНИЙ ЭТИ ЛИЦА СМЕНЯЮТСЯ.

Несмотря на внешнюю простоту, этот принцип оказался полезен при создании метода датировки. Принцип затухания частот имеет эквивалентную переформулировку. Так как персонажи практически однозначно определяются своими полными именами (имя = персонаж), то мы будем изучать резервуар всех полных имен текста. Термин «полное» будем обычно опускать, постоянно подразумевая его. Более того, оказалось, что подавляющее большинство исторических имен являются «простыми», состоящими из одного слова. Поэтому при обработке больших исторических текстов со значительным запасом имен можно рассматривать лишь «элементарные имена-кирпичи», разбивая редкие полные имена на отдельные составляющие их слова.

Рассмотрим группу всех имен, впервые появившихся в тексте, в «главе-поколении» с номером Q. Условно назовем эти имена Q-именами, а соответствующие им персонажи Q-персонажами. Количество всех упоминаний, с кратностями, всех этих имен в данной «главе» обозначим через K(Q, Q). Подсчитаем затем, сколько раз эти же имена упомянуты в «главе» с номером T. Получившееся число обозначим через K(Q, Т). При этом, если одно и то же имя повторяется несколько раз, то есть с кратностью, то все эти упоминания подсчитываются. Построим график, отложив по горизонтали номера «глав», а по вертикали — числа K(Q, T), где номер Q — фиксирован, а T — меняется. Для каждого Q мы получаем свой график. Принцип затухания частот тогда формулируется так.

При хронологически правильной нумерации «глав-поколений» каждый график К(Q, T) должен иметь следующий вид. СЛЕВА ОТ ТОЧКИ Q ГРАФИК РАВЕН НУЛЮ, В ТОЧКЕ Q — АБСОЛЮТНЫЙ МАКСИМУМ ГРАФИКА, ПОТОМ ГРАФИК ПОСТЕПЕННО ПАДАЕТ, БОЛЕЕ ИЛИ МЕНЕЕ МОНОТОННО ЗАТУХАЕТ, рис. 5.24.

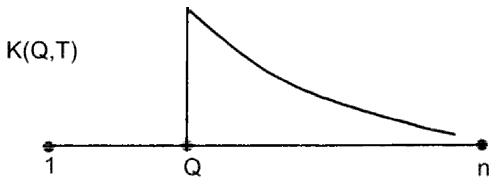
Рис. 5.24. Теоретический, «идеальный» график затухания частот.

Этот график на рис. 5.24 мы назовем идеальным. Сформулированный принцип должен быть проверен экспериментально. Если он верен и если «главы» в летописи упорядочены хронологически правильно, то все экспериментальные графики должны быть близки к идеальному. Проведенная экспериментальная проверка полностью подтвердила принцип затухания частот [904], [908]. Приведем некоторые типичные примеры.

Данный текст является ознакомительным фрагментом.