ГЛАВА ВТОРАЯ НАУЧНЫЕ ЗНАНИЯ ГЕОМЕТРИЯ ПИРАМИД

ГЛАВА ВТОРАЯ

НАУЧНЫЕ ЗНАНИЯ

ГЕОМЕТРИЯ ПИРАМИД

Мы видели, насколько осторожно следует относиться к различным высказываниям, касающимся поразительных, познаний, какими якобы обладали строители пирамид, даже тогда, когда эти высказывания исходят от авторов, научная репутация которых, казалось бы, должна была служить гарантией их добросовестности. Большей частью эти авторы, охваченные мистическим экстазом, который можно назвать наиболее точно «религией пирамид», потеряли чувство объективности и способность к критическому мышлению и направили все свои мысли на доказательство идей, явно предвзятых. Не колеблясь, они искажают реальные факты, когда в этом появляется хоть малейшая необходимость. Поэтому следует выяснить, особенно когда речь идет об астрономических и математических теориях, нет ли среди всей этой словесной шелухи каких-либо мыслей, заслуживающих внимания, ибо трудно предположить, что такое обилие гипотез не покоится хотя бы на какой-то доле истины.

Мы намереваемся изложить здесь выводы астрономического и математического порядка, действительно основанные на изучении конструкции и архитектуры пирамид, и попытаемся, когда в том представится необходимость, уточнить, в какой степени их особенности были предусмотрены египетскими строителями.

Прежде всего единственный неоспоримый с астрономической точки зрения факт, который можно установить в отношении этих памятников, в частности пирамид Гизе, — это чрезвычайная точность ориентировки. Наиболее поразительных результатов достигли строители пирамиды Хеопса, среднее отклонение которой не превышает 3?6?. Почти с такой же точностью ориентированы пирамиды Хефрена и Микерина, где отклонение составляет соответственно около 5?30? и 14?, т. е. здесь оно также минимально. Подобные приближения, повторяющиеся в ряде сооружений, не могут быть игрой случая и свидетельствуют об определенных астрономических познаниях. В частности, звезда, отмечавшая север в эпоху сооружения пирамид, должна была быть хорошо известна египтянам. Опираясь на эти знания, они сумели выработать практический метод ориентировки на земле, столь же простой, как и действенный, поскольку, вне всякого сомнения, в их распоряжении не было ничего, что могло бы выдержать сравнение с современными оптическими инструментами. Им приходилось довольствоваться обыкновенным шнуром с отвесом.

Возможно также, что при определении направления и наклона галерей пирамид для контроля производилось визирование некоторых звезд, хотя представляется более вероятным, что углы наклона сторон пирамиды устанавливались при помощи тригонометрической функции угла, как называют ее в настоящее время, в данном случае тангенса угла, или для угла О отношением h / b (рис. 39).

Действительно, из геометрических задач, приведенных в знаменитом математическом папирусе Ринд271 и комментариев к нему Борхардта272 вытекает, что египтяне принимали в качестве постоянной величину h, равную 1 локтю, состоящему из 7 пальм273, или 28 пальцев, и что они довольствовались этими мерами для выражения величины угла и для определения длины стороны b. Но это был общий метод, применяемый к углам произвольной величины. Мы увидим, что в противоположность этому египетские строители для осуществления своих колоссальных архитектурных замыслов стремились из практических соображений использовать в пределах возможного углы наклона, дающие для h/b простые отношения, не требующие деления и подразделения величины b на пальмы и пальцы. Так было, в частности, с углом наклона, избранным для коридоров и галерей Великой пирамиды, величина которого, составлявшая около 26,5°, соответствует b = 2 при h = 1, т. е., другими словами, наклону в ¹/₂. Этот довод неизмеримо более прост, чем утверждения некоторых астрономов, что нисходящий коридор был ориентирован по Альфе созвездия Дракона, близкой к полюсу и соответствующей его положению, правда в период, не совпадающий со временем правления Хеопса лет на пятьсот-шестъсот.

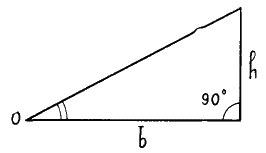
Рис. 39

По нашему мнению, астрономия при сооружении пирамид, за исключением их ориентировки, могла применяться лишь в ограниченных и достаточно гипотетических случаях. Однако бесспорно, что египтяне уже с эпохи строительства пирамид обладали некоторыми астрономическими представлениями, опирающимися на тысячелетние наблюдения за движением Солнца, Луны, планет («неутомимых»), звезд («вечных») и различных созвездий. Луна, по которой считали месяцы, в Египте в противоположность другим странам не привлекала к себе такого внимания астрономов, как Солнце и особенно звезды. Основная особенность египетской астрономии — это ее звездный характер. В частности, установление календаря — в эпоху, по-видимому, очень давнюю — основывается на точных наблюдениях годичного пути Солнца и положения Сотиса (Сириуса) по отношению к нему274. Равным образом имена декан, упоминаемые в Текстах пирамид, по-видимому, указывают, что цикл декан, позволяющий определять часы в ночное время, был уже в эту эпоху известен275.

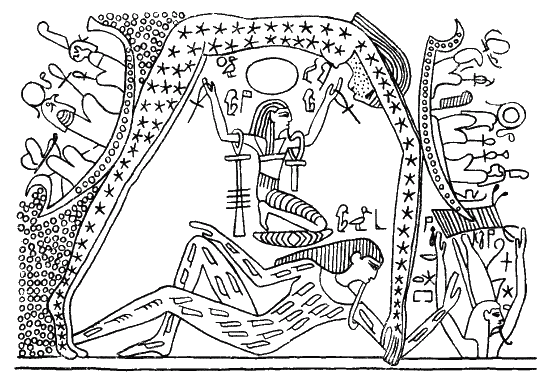
Рис. 40

Однако эти бесспорно замечательные наблюдения совершенно не доказывают, что египетские астрономы в эпоху строительства пирамид имели хотя бы малейшее представление о сферичности земного шара или о его движении вокруг Солнца. Для них Земля, олицетворенная в боге Гебе, была плоской, а под ней и в тесной взаимосвязи с нею находились адские глубины Дуата. Сверху, над Землей, небесный свод, поддерживаемый Шу, богом воздушного пространства, изображался в виде коровы или же в виде согнутой богини Нут, руки и ноги которой ограничивали пределы Земли (рис. 40). Солнечная ладья бога Ра, а также планеты, отождествляемые с божествами, плавали в небесном потоке вдоль тел обоих богов. Богиня Нут создавала таким образом для них небесный путь. Каждое утро она рождала Солнце, а вечером, завершив свой путь, Солнце исчезало у богини во рту и опускалось в адские пучины.

Даже принимая во внимание мифологические аллегории, мы все же видим, что представления египтян о мироздании были весьма далеки от наших. Кроме того, астрономические знания не являлись общим достоянием. Тесно связанные с мифологией, стремившейся установить зависимость между божествами, или потусторонними духами, и планетами, знания эти имели безусловно тайный характер. Обладателями их были лишь некоторые посвященные лица, возглавлявшие египетское жречество, и их приверженцы. В частности, в эпоху строительства пирамид главенствующую роль, по-видимому, играло жречество Гелиополя. Такое положение установилось во времена фараона III династии — Джосера, когда знаменитый Имхотеп, главный жрец Гелиополя и вместе с тем первый министр, выступал как главный архитектор при строительстве ступенчатой пирамиды и сооружений, расположенных внутри ее ограды. Во времена правления следующих династий это преобладание жречества Гелиополя, провозгласившего культ своего солнечного бога, еще более усилилось. Бог Солнца Ра, на происхождение от которого будут претендовать все фараоны, становится могущественнее Птаха, бога столицы — города Мемфиса, а также самого Осириса, или Анубиса, — повелителя царства мертвых — во всяком случае во всем, что относится к погребальному культу царей.

Таким образом, нет никаких оснований сомневаться в том, что жрецы-архитекторы обладали знаниями в области астрономии, особенно ярко проявившимися в ориентировке и планировке больших пирамид. Мы можем лишь выразить наше глубокое восхищение виртуозностью, с которой эти замечательные строители сумели приложить свои знания к разрешению сложных практических и технических задач, вызванных осуществлением на практике таких гигантских сооружений.

Изучение пирамид, с математической точки зрения, и особенно Великой пирамиды, открывает нам замечательные геометрические свойства, а также и некоторые численные соотношения, заслуживающие внимания. Но главная наша задача заключается в том, чтобы установить, в какой степени строители осознавали эти особенности. В частности, не ими ли, например, определялся выбор угла наклона, приданного пирамиде Хеопса? Или, наоборот, этот угол был избран в результате соображений чисто технического или практического порядка, которые неожиданно натолкнули на форму пирамиды, таящую в себе еще неизвестные свойства? Оба предположения выдвигались в течение многих лет, но, по-видимому, только теперь у нас появились данные, позволяющие решить этот вопрос.

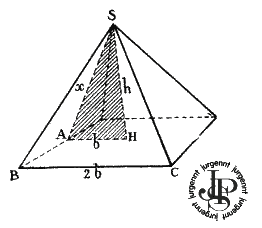
Рис. 41

Многие из геометрических соотношений, о которых идет речь, были известны еще в древности. Так, Геродот, основываясь на рассказах египетских жрецов, сообщает, что соотношение между длиной стороны основания и высотой Великой пирамиды такового, что квадрат, построенный на высоте пирамиды, равен площади каждой из ее сторон. Свойство это выражается равенством: h² = bx, где h обозначает высоту пирамиды, b — половину стороны ее основания, а x — апофему (рис. 41).

Это свойство может быть выражено так: «В прямоугольном треугольнике, который образован половиной среднего вертикального сечения пирамиды и гипотенуза которого служит одной из апофем, а одна из сторон, прилежащих к прямому углу, является высотой пирамиды, гипотенуза так относится к большему катету, как последний относится к меньшему катету»; т. е. х/h = h/b, откуда h² = bx (равенство Геродота).

Отношение золотого сечения между плоскостями пирамиды, установленное Клеппишем и приведенное выше, является также непосредственным следствием равенства Геродота. Согласно Клеппишу, площадь основания пирамиды S так относится к сумме площадей ее боковых граней S₁, как эта сумма относится к полной поверхности пирамиды S_t, т. е.

S/S_l = S_l/S_t

Так как квадрат основания и все треугольники имеют общее основание 2b, то достаточно написать пропорцию между половинами высот, т. е.

b/x = x/(b + x)

откуда b² + bx — x² = 0.

Следовательно, исходя из равенства Геродота h² = bх и теоремы Пифагора, дающей для треугольника SHA h² = x² — b² находим то же самое уравнение b² + bx — x² = 0, откуда получаем x/b = (1 + ?5)/2 = 1,618 = ?, т. е. отношение золотого сечения, численное значение которого выражается константой ? = 1,618, известной под названием «золотого числа».

Таким образам мы устанавливаем, что «золотое число» представлено в пирамиде отношением между апофемой и половиной стороны ее основания, что отметил еще Г. Ребер в 1855 г., т. е. выражением намного более простым, чем то, которое указывал Клеппиш. Свойства золотого сечения встречаются в любой пирамиде, имеющей соотношения, приведенные Геродотом. Нам остается лишь доказать, что эти соотношения свойственны Великой пирамиде.

Основные размеры, принятые для Великой пирамиды и исчисленные в египетских царских локтях по 0,524 м каждый (с избытком), составляют 440 локтей для стороны основания и 280 локтей для высоты пирамиды. Это дает в половине ее сечения по апофеме (т. е. в треугольнике SHA) простое отношение h/b=280/220=14/11, которое египтяне, следуя своему методу, выражали через b = 22 пальцам или, вернее, b = 5 пальмам + 2 пальца. Принимая за единицу измерения длины ¹/₁₁b, мы получаем b = 11, а из формулы h = b?((1+?5)/2), выведенной согласно теореме Пифагора и равенству Геродота, h = 13,992, т. е. 14 с точностью до нескольких тысячных.

С другой стороны, это отношение (14/11) дает сторонам пирамиды угол наклона в 51°50?35?, а отношение, о котором пишет Геродот, — 51°49?42? с отклонением примерно в 1?. Совершенно очевидно, что поверхность облицовки пирамиды в действительности не была совершенно гладкой. Будучи слегка волнистой, она давала местами значительно большее отклонение, чем указанное минимальное. Следовательно, мы вправе задать себе вопрос: можно ли было с простейшими инструментами египтян достигнуть в подобном случае точности, превышающей четверть или треть нашего градуса, т. е. 15 или 20?? Таким образом, точность значения отношения Геродота, из которого вытекают свойства золотого сечения, очень высока.

Что же касается отношения я, то мы приводим два наиболее часто упоминаемых: «Отношение периметра основания Великой пирамиды к ее удвоенной высоте равно ?, и отношение площади ее основания к площади среднего сечения равно ?».

Поскольку стороны пирамиды являются треугольниками одинаковой высоты, оба отношения приводятся к одному.

Пусть p — периметр основания. Полагая p = 8b, имеем

p/2h = 4b/h.

Если принять для отношения h/b ранее определенное значение 14/11, то получится: p/h = 4?11/14 = 22/7 = 3,1428 — приближенное значение ?. Таким образом, b/h = ?/4. Кроме того, мы имеем между ? и ? малоизвестное отношение: 0,618 = 1/? = (?/4)² = (3.1416/4)² = 0,617, т. е. 1/? с точностыо до одной тысячной.

С другой стороны,

x/b = Ф, x = Фb и b = x/Ф,

h² = bx = x²/? и x = h??,

откуда h/b = ?? = 4/?.

А так как h/b = 14/11, то ?? = 14/11, и следовательно, ? = 1,619.

Отметим еще, что если бы мы захотели получить точное значение ? = 3,1416, то для этого необходимо было бы увеличить угол наклона пирамиды на 40?, т. е. получить 51°51?14?. Угол этот Петри назвал «углом ?»276. Здесь также достигнуто совершенно поразительное приближение.

В итоге это можно свести к следующему.

Угол наклона 51°49?42? соответствует равенству Геродота и отношению золотого сечения.

Угол наклона, равный 51°50?35?, соответствует величине отношения апофемы к половине стороны основания, равной ¹⁴/₁₁, и дает ? = 3,1416.

Угол наклона, равный 51°50?39?, соответствует величине отношения ребра пирамиды к половине диагонали основания, равной ⁹/₁₀.

Угол наклона 51°51?14? дает ? = 3,1416.

Мы не будем принимать во внимание последний угол наклона, поскольку значение 3,1416 для ? было в ту эпоху неизвестно277. Максимальное расхождение между тремя первыми значениями ? составляет около 1?, что значительно меньше средней погрешности, допускаемой при производстве строительных работ. Эти три угла наклона могут, следовательно, рассматриваться как практически совпадающие, а пропорции и отношения, им соответствующие, как равновеликие.

В то же время очевидно, что при сооружении пирамиды для зодчего наиболее существенным представлялся выбор такого угла наклона сторон, который облегчил бы ее постройку и который легко было бы контролировать. Отношение h/b, т. е. отношение высоты к половине основания, определяющее форму пирамиды, должно было быть простым. Именно таким и являлось отношение ¹⁴/₁₁, принятое для пирамиды Хеопса. Что касается геометрических свойств, присущих всякой пирамиде, имеющей наклон ¹⁴/₁₁, то нам представляется крайне сомнительным, что они могли быть установлены зодчими Хеопса. Во всяком случае о «золотом числе» и отношении ? в то время, по всей вероятности, не имелось никаких представлений. С большими оговорками можно еще допустить, что в эпоху Хеопса было известно отношение, упоминаемое Геродотом.

Борхардт полагал, что на выбор зодчего повлияло только удобство отношения ¹⁴/₁₁. Нам представляется, однако, что не такое уж оно простое, чтобы его следовало принять безоговорочно. По нашему мнению, необходимо добавить, что оно соответствует, кроме того, с точностью до 4? более простому наклону в ⁹/₁₀, принятому для ребра пирамиды по отношению к диагонали основания. Одной из сложных проблем для строителей было определение угла наклона ребра, так как именно от него зависели очертания угловых камней, установка которых предшествует кладке облицовки и направляет ее. Этот наклон несомненно легко мог быть определен по углу наклона апофемы, но возможно, что тем не менее представлялось целесообразным определять и контролировать его непосредственно. Поскольку зодчие отдельных пирамид должны были отдать предпочтение углу наклона апофемы или углу наклона ребра, мы увидим, что они колебались в выборе и их усилия были явно направлены на определение угла наклона, дающего для проектирования — одновременно как по апофеме, так и по ребру — по возможности простые отношения.

В первоначальной мастабе Джосера, перекрытой впоследствии ступенчатой пирамидой, наружная облицовка имеет явно выраженный наклон в ⁴/₁, т. е. наиболее распространенный во многих мастабах, как это отмечает Петри. Что же касается самой ступенчатой пирамиды, то угол наклона ее сторон равен приблизительно 74° или h/b = 7/2. Египтяне, следуя своим правилам, выразили это отношение просто как b = 2 пальмам. Тот же угол наклона встречается затем в ступенчатой пирамиде в Завиет-эль-Ариане и на первых двух стадиях строительства пирамиды в Медуме. В третьей стадии эта пирамида, по всей вероятности являющаяся первой настоящей пирамидой, имеет уже угол наклона сторон 51°50?, который позднее будет использован и в пирамиде Хеопса.

После этой пирамиды были построены две большие пирамиды в Дашуре, возведенные, по-видимому, Снофру — отцом Хеопса. Первой была сооружена пирамида, находящаяся южнее, которую назвали «ромбовидной» из-за ее оригинальной формы, обусловленной изменением в процессе сооружения первоначального угла наклона ее сторон.

До высоты около 45 м этот угол, определенный более века назад Перрингом, равнялся 54°14?46?, соответствуя отношению h/b = 7/(5+1/25). У второй пирамиды в Дашуре, расположенной севернее, угол наклона апофемы (также по данным Перринга) составляет 43°36?, но, поскольку облицовка не сохранилась, приведенная цифра, возможно, приблизительна и, быть может, указывает на то, что принятый угол наклона мог как раз соответствовать углу наклона ²/₃ для ребра пирамиды. Было бы очень интересно проверить, не избрал ли Снофру еще раньше этот угол наклона и для верхней части своей первой пирамиды.

В пирамиде Хефрена, сооруженной после пирамиды Хеопса, сторонам придан более острый угол наклона. По данным Петри, он взял угол в 53°10?, очень близкий к 53°7?48?— углу знаменитого «священного треугольника» древности со сторонами, соответственно равными 3, 4 и 5. В этом случае построение сечения по апофеме, или отношение ⁴/₃ дает неоспоримое преимущество перед сечением по диагонали. Это ребро, однако, имея угол наклона несколько больше 43°, давало отношение высоты к половине диагонали ^8.5/₈, что почти так же легко реализуемо на практике, как и отношение Хеопса ⁹/₁₀. По нашему мнению, с точки зрения конструкции пирамида Хефрена была проще пирамиды Хеопса и северной пирамиды Снофру в Дашуре, в которых предпочтение было отдано построению угла для грани пирамиды, а не ее ребра.

Микерин, преемник Хефрена, также пытался найти для своей пирамиды наиболее удобный угол наклона. И, по-видимому, добился этого. Угол наклона сторон его пирамиды, с трудом определенный Петри из-за неровности поверхности облицовки, равняется приблизительно 51°10?, а угол в 51°20?25? соответствует египетскому треугольнику Виолле ле Дюка с катетами, равными 4 и 5. Поперечное сечение по апофеме дает, таким образом, простое отношение ⁵/₄, и при угле в 51°29?53?, который больше второго примерно на 9,5?, сечение по диагонали также даст простое отношение ⁸/₉.

Таковы были очертания первых пирамид фараонов III и IV династий. В заключение отметим, что после пирамиды в Медуме, где уже был взят наклон, позднее избранный и для пирамиды Хеопса, Снофру удалось найти для «ромбовидной» пирамиды угол наклона, дающий простые отношения для построения как апофемы, так и ребер пирамиды. Но так как в процессе строительства этот угол сочли чрезмерно острым, он был соответственно изменен. Затем, при сооружении верхней части этой пирамиды, второй пирамиды Снофру, и пирамиды Хеопса основная трудность, по-видимому, состояла в построении сечения по диагонали пирамиды. В пирамиде Хефрена, наоборот, основное место занимает построение сечения по апофеме. Но окончательного решения простых отношений как для апофемы, так и для ребер строители пирамид добились лишь в пирамиде Микерина; на этот раз они взяли угол наклона сторон не слишком острый, не слишком тупой.

В начале царствования V династии Сахура в Абусире пошел по тому же пути, что и зодчие пирамиды Микерина. Угол наклона сторон его пирамиды, определенный несколько приближенно Борхардтом в 50°5?, возможно, мог соответствовать углу в 50°11?40?, дающему при стороне основания в 150 локтей высоту в 90 локтей. Сечение по апофеме будет, следовательно, выражено простым отношением ⁶/₅, так же как и сечение по диагонали, которое составит простое отношение ⁶/₇.

Позднее, в период правления этой же династии, фараон Нефериркара в своей пирамиде возвратился к углу наклона сторон пирамиды Хефрена, а фараон Ниусерра — к углу наклона сторон пирамиды Хеопса. Наконец, на пирамидах VI династии, почти полностью разрушенных, мы сами обнаружили угол наклона около 53° в пирамиде Пепи II в Саккара. Здесь, следовательно, был вновь применен «священный треугольник» со сторонами 3, 4, 5, как и в пирамиде Хефрена. В период Среднего царства пирамида Сенусерта III в Дашуре при длине стороны 200 локтей имела угол наклона около 56°, что определяло ее высоту в 150 локтей, а угол наклона апофемы составлял ³/₂, что вновь дает чрезвычайно простое отношение.

Из этих разнообразных примеров мы заключаем, что но следует искать в пирамидах свидетельств необычайных познаний, наличие которых стремились доказать Жомар и его последователи. Жомар писал: «Из пропорций, бросающихся в глаза в этих памятниках, можно узнать законы, на основании которых их воздвигли; и поскольку они являются плодом египетской науки, то должны включать в себя ее элементы…» Однако анализ, приведенный выше, совершенно точно доказывает простоту этих законов и их элементов. Нам представляется, таким образом, весьма необдуманным допускать вместе с некоторыми другими, что пирамида Хеопса могла быть преднамеренным символическим выражением окружности, рассматриваемой как наиболее простая, совершенная фигура. Мы равным образом не верим и тому, что будто бы взятый Хефреном для определения угла наклона «священный треугольник» подтверждает намерение зодчего превратить эту пирамиду в его символическое выражение. Один из защитников данного положения вынужден был, однако, с этой точки зрения признать некоторый регресс после пирамиды Хеопса, каковую он расценивает как «шедевр их метода транспозиции», вплоть до пирамиды Микерина, по отношению к которой он задается вопросом: «Не остановился ли на этом уже достаточно усталый ум?!»278. Сравнительное рассмотрение значений углов наклона различных пирамид, наоборот, доказывает заметный прогресс вплоть до правления Микерина, при котором был взят угол наклона, определявший для граней и апофемы исключительно простые отношения.

Не кажется ли поэтому, что геометрия египтян предназначена лишь для удовлетворения технических и практических потребностей? Она разумно использует как некоторые прямоугольные треугольники, так и священный треугольник и определяет те стороны прямого угла, которые находятся между собой в таком же отношении, как два целых последовательных числа, например, 2 и 3, 4 и 5, 8 и 9, 9 и 10 и т. д., или же составляют простые отношения, как 1 и 4, 7 и 5, 11 и 14 и т. д.

Другие арифметические или геометрические отношения выражены в планировке внутренних помещений Великой пирамиды. Так, камера, названная усыпальницей фараона, в плане имеет 10 ? 20 локтей, высота же ее превышает 11 локтей на 9 см и составляет, следовательно, 11,172 локтя. Однако мы убеждаемся, что эта величина, не содержащая целого числа локтей, была, очевидно, получена в результате измерения диагоналей восточной и западной стен камеры, имеющих по 15 локтей. Мы получаем, таким образом, для каждой из этих диагоналей прямоугольный треугольник, основание которого, образованное меньшей стеной усыпальницы, было равно 2, гипотенуза — 3 и высота — ?5 = 2,236; а 2,236 ? 5 = 11,18, т. е. высоте с точностью примерно до ¹/₁₀₀ локтя279. Кроме того, длина в 15 локтей, выбранная для диагонали стены, влечет за собой наличие «священного треугольника» со сторонами, соответственно равными 3, 4 и 5, образованного в проходящей через эту диагональ плоскости продольного сеченпя камеры; подобное отношение мы получаем для диагоналей параллелепипеда этой камеры, равных 25 локтям.

Ф. Петри, основываясь на том, что один из трех размеров усыпальницы фараона не составлял целого числа локтей, счел возможным высказать предположение, что при определении размеров различных камер пирамиды (усыпальницы фараона, камеры царицы, подземных камер, передней), строители придерживались якобы правила, чтобы квадраты размеров этих камер равнялись целым числам квадратных локтей (это так называемая теория площадей). Приведенные нами выше более простые объяснения показывают, что не было никакой необходимости добиваться столь сложного решения для определения высоты усыпальницы фараона. Что же касается остальных камер, частью незаконченных, то обосновывать свои заключения на их размерах, особенно по их высоте, не имело смысла, поскольку вымостка плиточного пола не была завершена. «Передняя» же, как мы уже видели, никогда не служила камерой, а предназначалась лишь для размещения подъемных плит, преграждающих переход, и управления ими; поэтому определять ее размеры было совершенно бесполезно.

Вместе с тем многие отмечают, что вымостка пола усыпальницы фараона была якобы помещена на уровне, на котором площадь горизонтального сечения равнялась половине площади основания, а диагональ угла — одной из сторон основания. Из этих двух отношений, из которых одно является функцией другого, совершенно очевидно, что замысел строителей нашел свое отражение в соотношении площадей. Но египтяне, опытные геодезисты, безусловно знали, что площадь квадрата, построенного на диагонали, равна удвоенной площади первого квадрата. Используя данное правило, они легко определили уровень расположения погребальной камеры. Однако отсюда не следует, что из указанного свойства диагонали квадрата, являющегося лишь частным случаем для гипотенузы произвольного прямоугольного треугольника, египтяне сумели вывести основное отношение, получившее свое выражение лишь двадцать два века спустя после Хеопса в знаменитой теореме Пифагора.

В эпоху сооружения больших пирамид геометрия, таким образом, не выходила из стадии интуитивного и утилитарного эмпиризма. Жрецы-зодчие, поставленные перед трудными техническими задачами, изыскивают все более совершенные методы их разрешения; ум, все еще направленный на решение практических вопросов, не был способен целиком отдаться чисто отвлеченным исследованиям. Так были выработаны методы расчетов и построений, ссылки на которые встречаются в более поздних документах, как, например, в Папирусе Ринд или в Московском папирусе, относящихся к Среднему царству. Однако А. Рей280 спрашивает по поводу этих еще эмпирических текстов следом за Питом, так педантично опубликовавшим Папирус Ринд: «Не существовала ли геометрия более сокровенная, чем та, следы которой здесь имеются и позволяют иногда предполагать существование некоторых более остроумных решений, чем дошедшие до нас? Мы обнаружили бы тогда в сохранившихся папирусах лишь несколько полезных данных для тех, кому предстояло ими пользоваться».

Хотя до настоящего времени и не найдено никаких египетских математических документов сокровенного характера, все же, если верить грекам, известно, что египетские жрецы тщательно скрывали свои математические секреты. Аристотель указывает на то, что жрецы изучали математические науки, Диодор, как мы уже отмечали, сообщает об их влиянии на открытия и учение Пифагора и Демокрита, с гордостью провозглашавшего, что никто еще не опередил его в построении фигур при помощи линий и доказательстве их свойств, прибавляя при этом: «Даже египетские harpedonaptes281!»

Следовательно, вполне можно допустить, что египетские геометры действительно обладали обширными знаниями, тщательно собираемыми и секретно хранимыми в храмах, знаниями, полученными благодаря неусыпным наблюдениям в течение многих веков, отделяющих эпоху сооружения первых пирамид, т. е. около 2900 г. до н. э., от эпохи пробуждения математического мышления греков, т. е. начала VI в. до н. э. Что же касается, в частности, геометрии, то изучение таких сооружений, как знаменитая Великая пирамида, должно было занимать значительное место в исследованиях этих жрецов, и вполне понятно, что они сумели обнаружить в этих памятниках, без сомнения гораздо позже их сооружения, общие свойства, о которых не подозревали их строители.

Таким образом на протяжении трех тысячелетий своей древней истории Египет подготовил путь для открытий греческих ученых, накапливая постепенно сокровищницу знаний, из которой греческие ученые могли широко черпать необходимые сведения. Но все же нельзя отрицать, что лишь благодаря философски настроенному мышлению греков геометрия стала подлинной наукой.