Византийская математика

Византийская математика

Основным достижением математической мысли, характеризующим начало византийской математики, было возникновение и развитие понятия о доказательстве. Первым из философов, применившим в математике метод доказательства, считается греческий ученый Фалес из Милета. Фалес доказал, например, равенство вертикальных углов, равенство углов при основании равнобедренного треугольника, один из признаков равенства треугольников и т. д.

Новым было то, что Фалес впервые попытался логически свои выводы обосновать. Тем самым он положил начало дедуктивной математики – той, которая впоследствии была превращена в стройную и строгую систему знаний.

Затем метод доказательства был усовершенствован и развит учеными пифагорейской школы, которые доказали, в частности, утверждение, называемое теперь теоремой Пифагора. Пифагорейцы предприняли первую попытку свести геометрию и алгебру того времени к арифметике. Они считали, что «все есть число», понимая под словом «число» лишь натуральные числа.

Однако натуральных чисел и дробей оказалось недостаточно для того, чтобы выразить длину диагонали квадрата со стороной 1. Анализ полученного доказательства привел к исследованию начальных вопросов теории чисел (четности и нечетности натуральных чисел, разложения чисел на простые множители, свойств взаимно простых чисел и т. д.). Византийские математики эллинского периода предприняли попытку обосновать всю математику на основе геометрических понятий. Они истолковывали, например, сложение величин как сложение отрезков, а умножение – как построение прямоугольника с заданными сторонами.

Недостатком геометрического подхода к математике было то, что он препятствовал развитию алгебры. Византийцы умели в геометрической форме решать квадратные уравнения, но невозможно было представить геометрически четвертую и высшие степени длины, а кроме того, нельзя было складывать выражения разных степеней: эта сумма геометрического смысла не имела. По той же причине в византийской математике не было отрицательных чисел и нуля, иррациональных чисел и буквенного исчисления.

Пифагор первый заметил, что сила и единство науки основаны на работе с идеальными объектами. Например, прямая линия – это не тетива натянутого лука и не луч света: ведь они имеют небольшую толщину, а линия толщины не имеет. То же относится к геометрической плоскости и поверхности воды в спокойном озере или к числу 5 и пяти пальцам на руке. Идеальные объекты (будь то числа или фигуры) встречаются только в математическом рассуждении.

Все природные тела и процессы суть искаженные подобия идеальных тел и движений, а закономерности идеальных объектов выражаются с помощью чисел. Короче говоря: числа правят миром через свойства геометрических фигур! Но если так, то любые свойства чисел приобретают особое (даже мистическое) значение. Есть числа четные, а есть нечетные; есть простые и есть составные. И еще есть дроби, то есть отношения натуральных чисел; их Пифагор из осторожности называл не числами, а «величинами».

Так в школе Пифагора из арифметики была выделена в отдельную область теория чисел, то есть совокупность математических знаний, относящихся к общим свойствам операций с натуральными числами. В это время уже стали известными способы суммирования простейших арифметических прогрессий. Были рассмотрены вопросы делимости чисел, введены арифметическая, геометрическая и гармоническая пропорции.

Наряду с геометрическим доказательством теоремы Пифагора был найден способ отыскания неограниченного ряда троек «пифагоровых» чисел, то есть троек чисел, удовлетворяющих соотношению a ² + b ² = c ² и имеющих вид: п, (n ²-1)/2, (n ² + 1)/2, где п – нечетное. Было открыто много математических закономерностей теории музыки.

Едва ли не первой открытой иррациональностью явился 2 ^1/2. Можно предполагать, что исходным пунктом этого открытия были попытки найти общую меру с помощью алгоритма последовательного вычитания, известного под именем алгоритма Евклида. Возможно, что некоторую побудительную роль сыграла задача математической теории музыки: деление октавы, приводящее к решению пропорции 1: п = п: 2. Не последнюю роль, по-видимому, играл и характерный для пифагорейской школы общий интерес к проблемам теории чисел.

Вслед за иррациональностью2 ^1/2 были открыты многие другие иррациональности. Так, Архит доказал иррациональность чисел вида [n(n+1)] ^1/2. Теодор из Кирены установил иррациональность квадратного корня из чисел 3, 5, 6,…, 17.

Появление иррациональностей означало для неокрепшей греческой математики одновременное появление серьезных трудностей как в теоретико-числовом, так и в геометрическом плане. Была фактически поставлена под удар вся теория метрической геометрии и теория подобия. Но коль скоро открытие иррациональности показало, что совокупность геометрических величин (например отрезков) более полна, чем множество рациональных чисел, то представилось целесообразным это более общее исчисление строить в геометрической форме. Это исчисление было создано; в литературе оно получило название геометрической алгебры.

Первичными элементами геометрической алгебры являлись отрезки прямой: работой с ними были определены все операции исчисления. Сложение интерпретировалось приставлением отрезков, вычитание – отбрасыванием от отрезка части, равной вычитаемому отрезку. Умножение отрезков приводило к построению двумерного образа; произведением отрезков а и b считался прямоугольник со сторонами а и b. Произведение трех отрезков давало параллелепипед, а произведение большего числа сомножителей в геометрической алгебре не могло быть рассматриваемо. Деление оказывалось возможным лишь при условии, что размерность делимого больше размерности делителя. Оно интерпретировалось эквивалентной задачей приложения площадей. Метод приложения площадей был распространен и на случаи решения задач, сводящихся к квадратным уравнениям.

Однако довольно быстро выявилась ограниченность области применения методов геометрической алгебры. Средствами построения являлись только циркуль и линейка, и хотя можно представить себе операции с трехмерными образами, но даже такая простая, казалось бы, задача, как построение куба с объемом вдвое больше данного, не поддавалась решению с помощью циркуля и линейки. Задачи же, приводящиеся к уравнениям степени выше третьей, оказывались в геометрической алгебре просто невозможными.

Среди других задач, не имевших решения этими методами, наиболее известны проблемы трисекции угла и квадратуры круга.

История задачи об удвоении куба – пример того, как происходит обогащение математических методов. Из-за этой задачи конические сечения вошли в математику, став средством решения задач, не поддающихся циркулю и линейке. Впрочем, для решения задачи удвоения куба применялись и другие способы. Эратосфен, например, построил прибор (мезолабий), удобный для приближенного удвоения куба. Однако ни один из методов не имел столь большого влияния на развитие античной математики, как конические сечения.

Позже, с развитием алгебры, постановка задачи приобрела алгебраическую форму: может ли операция извлечения кубического корня из рационального числа быть сведена к конечному числу извлечений квадратного корня? Сомнение в возможности такого решения задачи высказал впервые в 1637 году Декарт. Но только еще через 200 лет задача удвоения куба получила окончательное разрешение. В 1837 году Ванцель доказал, что кубические иррациональности не принадлежат ни полю рациональных чисел, ни его расширению посредством присоединения квадратичных иррациональностей.

Второй знаменитой задачей античной древности была задача о трисекции угла, то есть о разделении произвольного угла на три равные части. Эта задача, как и предыдущая, сводится к решению кубического уравнения. Поэтому для нас полностью понятно, что многочисленные попытки произвести трисекцию угла с помощью только циркуля и линейки не могли быть успешными.

Трисекция угла имела столь же длинную историю, как и удвоение куба. Сведение ее к кубическому уравнению было осознано только в IX-Х веках н. э.

Третьей из знаменитых задач древности является квадратура круга, задача об отыскании квадрата, равновеликого данному кругу. Эту задачу в византийской античности рассматривали в обоих аспектах: точном и приближенном. Последний подход привел к введению приближения площади круга вписанными или описанными многоугольниками и к приближенным вычислениям числа «пи», но огромное количество попыток точно квадрировать круг к успеху привести не могли вследствие трансцендентной природы задачи.

Решение проблемы растянулось на много веков. Только в конце XVIII века И. Ламберт и А. Лежандр сумели доказать, что число «пи» не является рациональным числом. Трансцендентность же этого числа, то есть тот факт, что оно не может быть корнем никакого алгебраического уравнения с целыми коэффициентами, была доказана в 1882 году Линдеманом.

Византийские математики эллинского периода, стремившиеся теоретически точно решить задачу о квадратуре круга, этого, разумеется, не знали. Но их усилия принесли развитию математики большую пользу, обогатив ее новыми фактами и методами. Так, был разработан метод исчерпывания, являвшийся предшественником метода пределов. Были введены различные трансцендентные кривые. Наконец, впервые в истории математики были найдены квадрируемые фигуры, ограниченные кривыми линиями.

Появление иррациональностей обусловило необходимость создания общей теории отношений, способной дать определения и ввести операции, применимые как для рациональных, так и для иррациональных величин. Первоначальной основой этой теории стал алгоритм попеременного вычитания, известный как алгоритм Евклида.

В случае, если члены отношения соизмеримы, то алгоритм обрывается. Несоизмеримость не дает конечного алгоритма.

Однако попытка ввести операции над отношениями, определенными таким образом, сразу встретила серьезные математические трудности. Например, чтобы ввести умножение отношений, надо было найти способ определения неполных частных непрерывной дроби – произведения через неполные частные непрерывных дробей-сомножителей. Для этого и в наше время не существует никакой сколько-нибудь элементарной формулы. Наконец, в то время не существовало еще общего понятия величины. В силу этих обстоятельств алгоритм Евклида не сделался основой теории отношений.

На этом примере видно, что математические теории прошлого имеют зачастую много общего с современными математическими теориями. Однако надо учиться выделять специфику их исторического развития, чтобы не впадать в одну из двух ошибок: отождествления прошлого с настоящим или нигилистического отрыва настоящего от прошлого, того отрыва, который делает исследователя слепым перед контурами будущего.

Попытки систематизировать полученные при решении различных конкретных задач результаты предпринимались в византийской математике неоднократно. И успех, в отличие от других областей естествознания, был достигнут в математике потому, что она уже достаточно далеко ушла от реальности и научилась вычленять идеальные объекты и работать с ними. Что интересно, логика работала только в математике; когда хотели ее применить к обычной жизни, тут же сталкивались с различными противоречиями.

Абстрактность предмета математики и установившиеся приемы математического доказательства были основными причинами того, что математика стала излагаться как дедуктивная наука, представляющая логическую последовательность теорем и задач на построение и использующая минимум исходных положений. Сочинения, в которых в то время излагались первые системы математики, назывались «Началами».

Первые «Начала», о которых дошли до нас сведения, приписываются Гиппократу Хиосскому. Встречаются упоминания и о «Началах», принадлежащих другим авторам. Однако все эти сочинения оказались забытыми и утерянными практически с тех пор, как появились «Начала» Евклида, которые получили всеобщее признание как система математических знаний, логическая строгость которой оставалась непревзойденной в течение очень большого времени. Его «Начала» до сих пор лежат в основе всех систематических школьных курсов геометрии. Научные исследования по математике, в особенности элементарной, в очень большой степени опираются на систему Евклида, иногда подражая даже форме его изложения.

В «Началах» тринадцать книг, каждая из которых состоит из последовательности теорем. Иногда к этим книгам добавляют книги №№ 14 и 15, принадлежащие другим авторам и близкие по содержанию к последним книгам Евклида. Первой книге предпосланы определения, аксиомы и постулаты. Определения имеются и в некоторых других книгах (2–7, 10, 11). Аксиом и постулатов в других книгах «Начал» нет.

Определения – это предложения, с помощью которых автор вводит математические понятия путем их пояснения. Например, «точка есть то, что не имеет частей», «куб есть телесная фигура, заключающаяся между шестью равными квадратами» и т. п. Эти предложения Евклида много раз подвергались критике с точки зрения их полноты и логической определенности, однако равноценной или более совершенной системы определений предложено не было.

Дело свелось к тому, что в наше время при аксиоматическом построении математической теории единственным способом описания объектов этой теории и их свойств является сама система аксиом, а объекты вводятся как первичные неразъясняемые сущности. Что же касается определений Евклида, то их следует рассматривать как исторически сложившиеся к его времени абстракции реальных вещей, введение которых в математику освящено традицией. Это – не такой уж редкий, если не сказать наиболее часто встречающийся в истории способ введения математических определений.

В различных изданиях «Начал», а ранее того переписчиками и комментаторами, система аксиом и постулатов Евклида видоизменялась и дополнялась. То, что мы имеем ныне, если угодно, результат большого количества проб и ошибок многих исследователей. Так что, как и многие книги того времени, Евклид – это не имя человека, а некое название труда.

«Начала» Евклида в течение многих веков служили классическим образцом математической строгости и последовательности. Однако были здесь и неблагоприятные для дальнейшего развития математики факторы. Изложение – чисто геометрическое, даже числа представлены как отрезки. Средства геометрического построения, по существу, ограничены только циркулем и линейкой. В «Началах» нет теории конических сечений, алгебраических и трансцендентных кривых, отсутствуют вычислительные методы.

Тем временем при построении математических теорий в Византии выделился специфический класс проблем, для решения которых оказалось необходимым исследовать предельные переходы, бесконечные процессы, непрерывность и т. п. Появилась математика атомистических философских воззрений. Согласно этим взглядам, все тела состоят из бесконечно малых атомов – первовеличин. Эти идеи стали источником представлений о бесконечно малых и о применении их к определению геометрических величин.

Однако о математической стороне подобных высказываний и исследований почти ничего неизвестно. Гораздо больше известно о возражениях противников этих идей. Мы имеем в виду апории Зенона, те логические парадоксы, к которым приводят попытки получать непрерывные величины из бесконечного множества бесконечно малых частиц.

Среди апорий наиболее известны: а) дихотомия, то есть невозможность осуществить движение, так как путь может быть делим до бесконечности (пополам, еще раз пополам и т. д.) и поэтому надо последовательно преодолевать бесконечное множество участков пути; б) Ахиллес, который не может догнать черепаху, так как ему надо последовательно достигать тех мест, где только что находилась черепаха, тем самым исчерпывать бесконечную последовательность отрезков пути; в) полет стрелы делается невозможным, если время считать суммой дискретных мгновений, а пространство – суммой дискретных точек.

Апории Зенона показывали, что, если искать точные доказательства и логически исчерпывающие решения задач, нельзя пользоваться бесконечностью, опираясь на наивные атомистические соображения. Для подобных целей необходимо разрабатывать и привлекать методы, содержащие наряду с разновидностями суждений о бесконечно малых элементы предельного перехода.

Одним из самых ранних методов такого рода является метод исчерпывания. Изобретение его обычно приписывают Евдоксу, а примеры употребления находятся в двенадцатой книге «Начал» Евклида и в ряде сочинений Архимеда. Метод исчерпывания применялся при вычислении площадей фигур, объемов тел, длин кривых линий, нахождении подкасательных к кривым и т. п.

Однако метод был еще весьма несовершенным; и он развивался только в связи с конкретными задачами. Он не приобрел вида абстрактного метода, имеющего развитую систему исходных понятий и единообразные алгоритмы. Единственность предела доказывалась для всякой задачи заново. Этот недостаток не был частным, случайным. Дело в том, что всякая попытка ввести доказательство раз и навсегда для определенного, достаточно широкого класса задач неизбежно влекла за собой необходимость дать рациональное объяснение понятию бесконечно близкого приближения, бесконечно малой величины и т. п. Трудностей, связанных с этим, математики того времени не могли преодолеть.

Тем не менее метод исчерпывания лежал в основе многих конкретных достижений античных математиков, в первую очередь приписываемых Архимеду. До нас дошли десять сравнительно крупных и несколько мелких его сочинений математического характера, написанных преимущественно в виде писем. Основной их особенностью является применение строгих математических методов к разработке экспериментально-теоретического материала из области механики и физики. И вот, в соответствии с научной традицией своего времени Архимед переводил доказательства, полученные методом механической аналогии, на общепринятый язык метода исчерпывания с обязательным завершением последнего, в каждом отдельном случае, доказательством от противного.

Следующей разновидностью методов бесконечно малых является метод, который можно охарактеризовать как метод интегральных сумм. Наиболее яркие примеры применения этого метода находятся в сочинениях Архимеда: «О шаре и цилиндре», «О спиралях», «О коноидах и сфероидах». Сущность этого метода в применении, например, к вычислению объемов тел вращения состоит в следующем: тело вращения разбивается на части и каждая часть аппроксимируется описанным и вписанным телами, объемы которых можно вычислить. Сумма объемов описанных тел будет больше, а сумма вписанных тел – меньше объема тела вращения. Теперь остается выбрать аппроксимирующие сверху и снизу тела таким образом, чтобы разность их объемов могла быть сделана сколь угодно малой. Это достигается выбором в качестве указанных тел соответствующих цилиндриков. Единственность предела доказывается, как и во всех других случаях, приведением к противоречию.

Может показаться, что метод интегральных сумм древних и метод определенного интегрирования имеют много общего. Это происходит оттого, что мы излагаем тему современным языком. Но это не так.

Метод интегральных сумм древних опирается на интуитивное, строго не определенное понятие площади и не использует арифметико-алгебраического аппарата. В нем не введены и не определены необходимые общие понятия: предела, интеграла, бесконечной суммы, и не изучены условия применимости высказываемых теорем. Словом, метод применяется индивидуально для каждой конкретной задачи без выделения и оформления его общетеоретических основ.

Наряду с методом интегральных сумм в математике были разработаны и другие, которые ретроспективно могут быть оценены как дифференциальные методы. Примером может служить метод нахождения касательной к спирали в сочинении Архимеда «О спиралях».

Но широкое использование этот метод получил значительно позже, когда в XVI–XVII веках Паскаль, Барроу и Лейбниц создавали свое исчисление дифференциалов. Поэтому не исключено, что работы Архимеда имеют даже существенно более позднее происхождение, чем мы можем предположить. Ведь они послужили исходным пунктом многих исследований ученых-математиков XVI и XVII веков. Лейбниц, один из основателей математического анализа, по этому поводу писал: «Изучая труды Архимеда, перестаешь удивляться успехам современных математиков».

Вернемся к коническим сечениям. Интерес к ним возрастал по мере увеличения количества решаемых с их помощью задач. Свойства конических сечений стали предметом специального теоретического исследования; им был посвящен ряд сочинений. Однако, подобно тому, как это имело место и с «Началами» Евклида, все эти сочинения были забыты, когда появился труд александрийца Аполлония «Конические сечения».

Первые четыре книги этого труда сохранились на греческом языке, следующие три в арабском переводе, а последняя книга утеряна. Аполлоний первым ввел эллипс, параболу и гиперболу как произвольные плоские сечения произвольных конусов с круговым основанием и детально исследовал их свойства. Метод Аполлония состоял в отнесении кривой к какому-либо ее диаметру и сопряженным с ним хордам и предвосхищал созданный в XVII веке метод координат. «Конические сечения» Аполлония оказали огромное влияние на развитие наук Нового времени – астрономии, механики, оптики. Из положений Аполлония исходили при создании аналитической геометрии Декарт (1596–1650) и Ферма (1601–1655).

Мы видим, что большинство математических теорий до какого-то времени имело своим предметом геометрические объекты. Дело в том, что геометрические величины представлялись имеющими преимущество наибольшей общности в классе математических величин. Хотя, разумеется, нет оснований утверждать, что геометрические формы исчерпывали всю совокупность форм математической деятельности. Греки Византии в практической области применяли большой комплекс арифметико-вычислительных методов. Этот комплекс проникал и в теоретические работы, дополняя теорию арифметико-алгебраическими и теоретико-числовыми элементами.

Но неудобства алфавитной системы счисления и неразработанность символов мешали развитию вычислительных операций. Да и требования практики не были достаточными, чтобы стимулировать операции с весьма большими числами. Вслед за сравнительно ограниченным набором чисел, имеющих названия, довольно быстро наступал порог, после которого число элементов практически представлялось неисчислимым.

Чтобы устранить подобное несовершенство и показать неограниченную продолжаемость натурального ряда чисел, Архимед написал специальное сочинение под названием «Псаммит» (исчисление песка), в котором показывается, что система чисел может быть продолжена сколь угодно далеко и может служить для пересчета любого конечного множества предметов.

Система чисел Архимеда построена по десятичному принципу: единицы (монады), десятки (декады), сотни (гекады), тысячи (хилиады), десятки тысяч (мириады) и т. д. Мириада затем рассматривается как основа счета до числа мириады мириад (10⁸). Числа от 1 до 10⁸ образуют первую октаду (от слова восемь), а числа, в нее входящие, называются первыми. Далее следуют вторая октада, третья и т. д., до октады чисел октадных, замыкающей первый период. Она является исходной единицей второго периода, далее следуют единицы чисел третьего периода, четвертого и так до октады чисел октадных октадного периода.

Получающиеся огромные числа воспринимались как своеобразные бесконечности, шкала роста которых могла быть неограниченно продолжаема. Их с избытком хватало даже для такой задачи, как определение порядка числа песчинок, могущих полностью заполнить всю Вселенную.

Чтобы сделать задачу возможно более определенной, Архимед, исходя из гелиоцентрических воззрений Аристарха Самосского, представляет Вселенную как шар, в центре которого находится Солнце. Радиус шара считается от Солнца до неподвижных звезд. Для дальнейшего уточнения задачи принимается, что диаметр Вселенной во столько же раз больше диаметра Солнечной системы, во сколько раз этот последний больше диаметра Земли. Архимед использует экспериментальные данные астрономов, округляя их в сторону увеличения.

Единица измерения Вселенной – песчинка, принята за 0,0001 зернышка мака, которых требуется 40 штук, чтобы сравняться с шириной человеческого пальца. Подсчеты, произведенные Архимедом, показали, что искомое число песчинок будет не больше чем 10⁶³, или тысячи (10³) мириад (10⁴) чисел восьмых (10⁷⁸) первого периода.

Однако уровень вычислительно-практических приложений многих развитых математических теорий оставался все же сравнительно низким. Это объясняется оторванностью от практики, принудительностью геометрической формы, ограничением совокупности применяемых методов, отсутствием тригонометрии. Требования астрономии к математике с достаточной силой сказались несколько позже.

Официальная история удивляется, что после Евклида, Архимеда и Аполлония наступило время как бы деградации византийской математики. Такой взгляд происходит от неправильного понимания авторства и времени написания этих трудов.

Считается, что после разгрома Александрийского научного центра в VI веке остался последний центр античной науки – Афины, который так же был со временем разгромлен. На самом деле «переезд науки» в Афины – это история Афин под властью крестоносцев, XIII–XV веков. Здесь произошла встреча западноевропейской, арабской и остатков византийской культуры.

В более позднее время постепенно интерес смещается в сторону практических вычислительных методов и задач. Образцом работ подобного направления являются математические работы Герона из Александрии, в особенности его «Метрика». Стиль последней – рецептурный: для определенных классов задач формулируются правила, справедливость которых подкрепляется примерами.

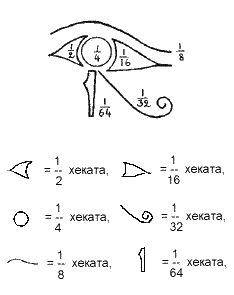
Египетские дроби, записанные для лучшего запоминания в виде «глаза Ра»

В «Метрике» содержатся правила для точного и приближенного определения площадей геометрических фигур и объемов тел, правила численного решения квадратных уравнений и извлечения (преимущественно приближенного) квадратных и кубических корней. В частности, в ней приводится известная формула Герона для вычисления площади треугольника по трем его сторонам

S = [р(р-а)(р-b)(р-с)] ^1/2,

где а, b, с – стороны, p= (а + b + с)/2.

Наконец, значительную часть содержания «Метрики» составляет описание приемов землемерия и геодезических инструментов.

Значение прикладной вычислительной стороны математики еще более подчеркивается той большой и все возрастающей работой, которую математики вынуждены были вести для составления астрономических таблиц. Среди последних особо значительное место занимают таблицы хорд Птолемея, где данные приведены через каждые 30 от 0 до 180°.

На основе преимущественного роста вычислительной стороны математики, а возможно и под другими дополнительными влияниями в математике зародились элементы алгебры и начальные формы алгебраической символики. На это обстоятельство указывают методы и результаты Диофанта. Из математических сочинений этого александрийского ученого сохранились шесть книг «Арифметики» и отрывки книги о многоугольных числах. Диофант во всех задачах производит только операции с числами, нигде не высказывая общих теорем. Тем не менее для обозначения неизвестного количества в уравнении и для записи функций от него он был вынужден разработать систему символов.

Символика Диофанта основана на сокращении слов, и в истории развития алгебраической символики она знаменует переход от словесных выражений алгебраических зависимостей (риторическая алгебра) к сокращениям этих выражений (синкопическая алгебра). Следующей ступенью развития стала чисто символическая алгебра.

Неизвестная величина х в уравнениях Диофанта представлена специальным символом. Переписчики, впрочем, пользовались разными символами, что не изменяет принципиально существа дела, ибо символика не строго единообразная, имеет модификации.

Общая теория диофантовых уравнений первой степени ах+b=1, где а и b – взаимно простые целые числа, была построена в XVII веке французским математиком Баше де Мезириаком (1587–1638). Он также издал в 1621 году сочинения Диофанта на греческом и латинском языках со своими комментариями. Над созданием общей теории диофантовых уравнений 2-й степени трудились многие выдающиеся ученые: П. Ферма, Дж. Валлис, Л. Эйлер, Ж. Лагранж и К. Гаусс. В результате их усилий к началу XIX века было в основном исследовано общее неоднородное уравнение 2-й степени с двумя неизвестными и с целыми коэффициентами.

Имя Диофанта прочно закрепилось и в той части теории чисел, которая изучает приближения действительных чисел рациональными числами; эти приближения так и называются диофантовыми.

Историки науки отмечают, что после закрытия афинской школы в бассейне Средиземноморья в развитии математики как науки наступил длительный перерыв. Но мы помним, что это за афинская школа. Это как раз время заката Византийской империи, и подтверждением тому – тот неоспоримый факт, что в рамках математических теорий «античной древности» возникли и развивались элементы более поздних математических наук: алгебры, анализа бесконечно малых, аналитической геометрии, теоретической механики, аксиоматического метода в математике.

Если сравнивать разные «части» традиционной истории, сразу видно, что умением плавать по морю и строить города ромеи (византийцы) не уступали своим предкам-эллинам; в государственных делах они также были впереди многих государств. И при этом историки науки нам говорят, что ромеи не унаследовали от эллинов любовь к натурфилософии и к точным наукам. Оказывается, для них главным видом интеллектуальной деятельности стало богословие. Монахи и императоры косо смотрели на «языческую премудрость» эллинов. И в завершение ликвидировали последний оплот знания – Академию в Афинах.

В результате возникает необъяснимый феномен: тысячелетняя Византийская империя, не знающая математики. Но загадки нет, если правильно понять, где и когда развивалось то, что мы называем математикой Древней Греции.

Данный текст является ознакомительным фрагментом.