Мы сами составляем карты

Перед вами глобус. Как по нему составить карту какого-либо материка, допустим, Африки? Прежде всего выберем проекцию и построим соответствующую ей картографическую сетку в определенном масштабе. Возьмем наиболее простую проекцию — квадратную. На листе бумаги проведем две взаимно перпендикулярные линии. Вертикальную линию будем считать нулевым меридианом, а горизонтальную — экватором. Через равные интервалы проведем параллельные им линии, образующие квадраты. Стороны квадратов, т. е. расстояния между параллельными линиями, зависят от оцифровки параллелей и меридианов и масштаба карты. Предположим, мы хотим составить карту в масштабе 1:50 000 000 (по экватору и меридианам) с густотой картографической сетки 10°. В таком случае сторона квадрата составит 2,22 см (1110 км:50 000 000).

Пользуясь вычерченной сеткой параллелей и меридианов, перенесем с глобуса по соответствующим клеткам контур береговой линии африканского материка.

В пределах каждой клетки рисунок переносится на глаз. Чтобы береговая линия не была ломаной, нужно вначале наметить точки ее пересечения со сторонами клетки, а затем их соединять, учитывая общий изгиб линии.

По картографической сетке можно проверить правильность перенесения береговой линии на карту путем сличения координат соответствующих точек. Так, координаты крайних точек Африки следующие: северной — мыс Эль-Абьяд (37° с. ш., 10° в. д.); южной — мыс Игольный (35° ю. ш., 20° в. д.); западной — мыс Альмади (18° з. д., 15° с. ш.); восточной — мыс Хафун (51° в. д., 10° с. ш.)

Составим еще одну карту — карту Австралии в цилиндрической проекции, но за основу возьмем не глобус, а карту восточного полушария (рис 20, а).

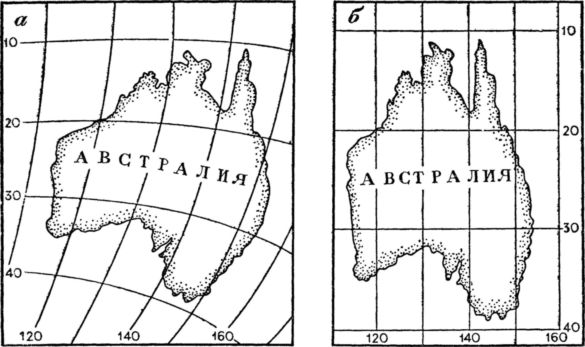
Рис. 20. Изображение Австралии на карте полушария (а) и на карте в цилиндрической проекции (б).

Картографическая сетка для нашей карты будет прямоугольной с соотношением сторон клеток 1:2, например, отрезок меридиана в 10° широты будет соответствовать 2 см, а параллели в 10° широты — 1 см. Вычертим рамку карты, и у ее сторон подпишем широты и долготы у соответствующих параллелей и меридианов (рис. 20, 6). Контур материка будем переносить более точно — по опорным пунктам. Для этого на исходной карте определим координаты точек пересечения береговой линии с меридианами или параллелями и направление береговой линии в этих точках (табл. 2).

Таблица 2

Координаты точек пересечения береговой линии с меридианами и параллелями

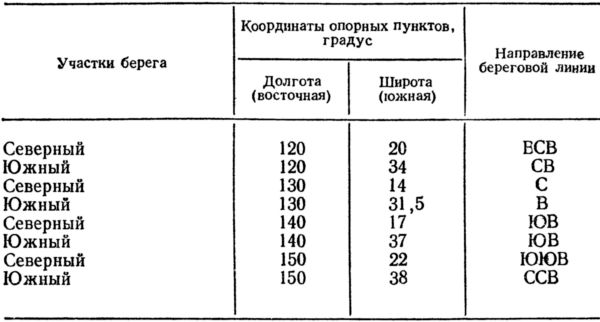
По координатам нанесем на картографическую сетку опорные пункты и от них на глаз перенесем береговую линию со всеми ее изгибами. Опорные пункты дают возможность более точно перенести с исходной карты контур материка на карту, составляемую в другой проекции.

Сравните очертания Австралии в обеих проекциях. Если в первой проекции (см. рис. 20, а) общий вид материка примерно соответствует действительной конфигурации, то во второй проекции (рис. 20, 6) изображение получилось сжатым по долготе и вытянутым по широте. И тем не менее в обеих проекциях очертание береговой линии со всеми ее подробностями остается постоянным и географические координаты каждого ее изгиба будут одинаковыми.

Приведем еще пример преобразования одной картографической проекции в другую. Исходной картой будет карта СССР в конической проекции (рис. 21, a), a по ней нам нужно составить такую же карту, но в цилиндрической проекции (рис. 21, 6).

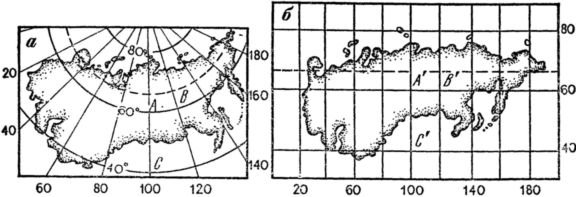
Рис. 21. Карта СССР в конической (а) и цилиндрической (б) проекциях.

Здесь по сути дела задача сводится к тому, чтобы растянуть дуги параллелей в прямые линии. А практически решается она так. Нанесем параллельно друг другу три прямые линии, которые обозначают параллели 40, 60 и 80°. Расстояния между ними равны соответствующим расстояниям на исходной карте (А'С' = АС). На параллели 60° отложим отрезки между меридианами (А'В' = АВ) и от точек отложения проведем линии, перпендикулярные к параллелям. Они будут меридианами. На построенную картографическую сетку перенесем по клеткам сухопутные и морские границы страны. Можно уточнить их положение путем отложения одинаковых расстояний по меридианам от 60-й параллели.

Обратите внимание на конфигурацию изображений в той и другой проекции: какие они разные! Взять, например, общее направление побережья Северного Ледовитого океана. На первой карте оно имеет вогнутый вид, а на второй — получилось выпуклым.

Картографы могут предложить множество проекций, причем каждая из них будет удовлетворять заданным условиям. Попытаемся и мы решить такую задачу. Допустим, нам потребовалась проекция карты, которая имела бы одинаковый масштаб по экватору и по всем меридианам, но в отличие от цилиндрической квадратной проекции, где это условие соблюдается, географические полюса в нашей проекции должны изображаться точками.

Для построения картографической сетки в данной проекции проведем линию экватора и отложим на ней равные отрезки, соответствующие определенному числу градусов долготы, например 30° (рис. 22).

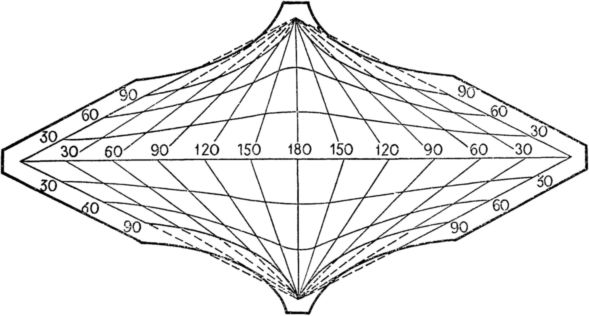
Рис. 22. Проекция, в которой сохраняется одинаковый масштаб по экватору и всем меридианам.

Через середину линии экватора восставим перпендикуляр и отложим на нем вверх и вниз по три таких же отрезка, как и на экваторе. Вершины перпендикуляров соединим прямыми линиями со всеми точками деления на экваторе. Получились меридианы. Согласно условию задачи, масштаб по экватору и меридианам должен быть одним и тем же. Чтобы выполнить это условие, отложим на меридианах по три отрезка, равных отрезкам на экваторе и меридианах. Соответствующие точки на перпендикуляре и наклонных линиях соединим плавными линиями. Эти линии будут параллелями, построенными через 30° по широте. Таким образом, у нас получилась картографическая сетка, удовлетворяющая тем же условиям, что и сетка в квадратной проекции, а в вершинах меридианов находятся географические полюса.

В кратком историческом очерке создания карт вы познакомились с картографическими изображениями, построенными исключительно условно. Это арабские карты. Конфигурация материков и морей передается на них в виде геометрических фигур: окружностей, квадратов, треугольников и др. Составим и мы такую «карту» и попытаемся установить, не заложены ли в них какие-либо основы картографического проектирования.

На рис. 23, а изображена карта острова Калимантан. Разделим береговую линию острова точками A, B, C и D на четыре равных части и, спрямив их, построим квадрат A'B'C'D' (рис. 23, 6).

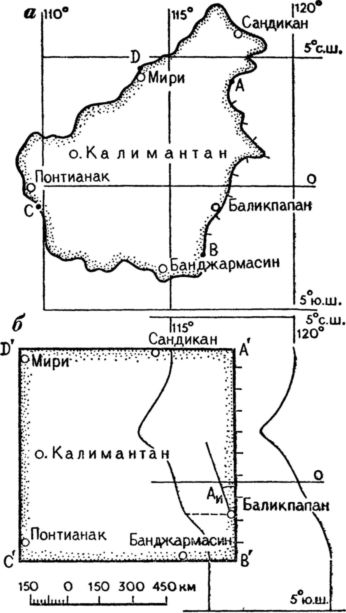
Рис. 23. Карта острова Калимантан (а) и составленная по ней карта в виде квадрата (б).

Понятно, что периметр квадрата будет равен всей длине береговой линии. Перенесем прибрежные населенные пункты на стороны квадрата. Для этого разделим каждый участок береговой линии и стороны квадрата на одно и то же число равных интервалов. В нашем примере участок побережья АВ и сторона квадрата А'В' разделены на 10 частей. Пользуясь идентичной шкалой равных отрезков, нанесем на нашу «квадратную карту» населенные пункты и подпишем их названия.

Составленная нами карта необычна для восприятия, но ею с успехом можно пользоваться при плавании, когда корабли курсируют между прибрежными населенными пунктами, не удаляясь далеко от берега. Она имеет даже некоторые преимущества перед обычной: по ней значительно легче и быстрее можно определить расстояние между любыми пунктами, расположенными на побережье. На такую карту можно нанести для любой стороны квадрата и картографическую сетку. Нанесем ее, например, для стороны А'В'. Крайние параллели пройдут от точек А' и В' на расстояниях, измеренных по карте от точек A и В, а средняя параллель пройдет между идентичными штрихами. Линии меридианов изогнутся в зависимости от конфигурации береговой линии. Наносятся они путем откладывания расстояний по параллелям от точек А' и В' и каждого штриха. Эти расстояния соответствуют расстояниям, измеренным на карте от соответствующих точек и штрихов до меридианов. Отложенные точки соединяются плавными кривыми. Координаты населенного пункта Баликпапан, определенные по нашей «карте», составят 1° ю. ш. и 117° в. д., т. е. получились такими же, как и снятые с обычной карты.

Построенная картографическая сетка для стороны АВ позволяет определить не только координаты прибрежных объектов. Перенеся линию меридиана к какой-либо точке на берегу, можно измерить угол от северного конца меридиана до направления береговой линии. Этот угол называется азимутом; им пользуются при вождении кораблей с помощью компаса. Так что наша карта имеет ряд картографических признаков, которые дают возможность пользоваться ею для практических целей. Вероятно, подобные признаки были заложены и в арабских картах. Частично раскрыть тайны этих карт удалось польскому ученому Иохиму Лелевелю, жившему в первой половине XIX в. По старым арабским рукописям и таблицам он расшифровал карту мира и представил ее в виде обычной карты, доступной современникам.