Решение задач по топографической карте

Из всех географических карт топографические карты — самые точные и подробные. По ним можно определить, например, не только точные географические координаты различных пунктов, но и прямоугольные. Для удобства пользования прямоугольными координатами на каждом листе топографической карты имеется сетка квадратов, которую называют километровой. Она образована взаимно перпендикулярными линиями, проведенными через 2, 4 или 10 см. У всех линий километровой сетки даны подписи координат, которые необходимы не только для нанесения пунктов по заданным координатам, но и для отыскания объектов на карте. Для этого вначале указывают число, подписанное у нижней горизонтальной стороны квадрата, в котором расположен пункт, а затем у левой вертикальной.

Действительную наглядную картину местности создают на топографической карте с помощью условных знаков. Без знания условных знаков невозможно прочитать карту, также, как нельзя прочитать книгу, не зная букв. Условные знаки, принятые для наших топографических карт, просты, удобны для запоминания и в большинстве своем имеют начертание, напоминающее внешний вид изображаемого предмета местности.

К изобразительным свойствам условных знаков, кроме внешнего подобия, относится и цвет. Он придает карте красочность, наглядность, позволяет обогатить ее содержание. Цвета, принятые для некоторых условных знаков, соответствуют окраске изображаемых объектов. Так, лесные массивы, кустарники, сады и парки изображают зеленым цветом; моря, реки, озера, источники — голубым; элементы рельефа — коричневым. Это — традиционные цвета, применяемые на картах всего мира. Другие цвета имеют меньшее распространение.

В своем начертании условные знаки имеют такие элементы, которые позволяют определять точное местоположение любого объекта. Ими являются точки и линии контуров, осевые линии дорог и главные точки внемасштабных условных знаков, находящиеся в строго определенных местах значков в зависимости от их формы (в центре знака, середине основания или вершине угла).

Обратите внимание: условные знаки отдельного дерева, ветряного двигателя, бензоколонки и некоторых других предметов имеют у основания подсечку в виде черточки, направленной вправо. Эта подсечка имеет давнюю историю. Когда-то для наглядности карты условные знаки оттенялись. Оттенение их производилось в определенном порядке, принимая во внимание условное освещение местности с северо-запада на юго-восток. На топографических картах север находится наверху, а запад слева, поэтому изображаемые местные предметы предполагались освещенными сверху и слева. При таком условном освещении стороны предметов, находящихся в тени, изображались утолщением их очертаний. У возвышенных предметов оттенялись правые и нижние стороны. Углубленные предметы, такие, как реки, пруды, озера, оттенялись утолщением их левых и верхних берегов.

А как же оттенять внемасштабные условные знаки, у которых имеется всего одна вертикальная линия? Вот для них в то время и условились давать у основания небольшую подсечку вправо, которая изображает как бы тень от предмета.

Основу содержания топографических карт составляют графические условные знаки. В дополнение к ним для качественной характеристики предметов местности применяют буквенно-цифровые обозначения. Они дают возможность более объективно оценить тот или иной объект местности. Вот, например, что можно узнать о реке по буквенно-цифровым обозначениям: ширину, глубину и скорость течения реки, характер грунта дна, глубину бродов, размеры и грузоподъемность мостов, паромов.

По буквенно-цифровым обозначениям можно решать различные практические задачи. Например, пусть на территории области протекают две реки: Шуя и Сан (рис. 42).

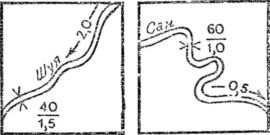
Рис. 42. Какая река более полноводна?

Какая из рек более полноводна и на какой можно построить более мощную гидроэлектростанцию?

Для решения задачи нужно прежде всего знать среднюю скорость течения воды в каждой реке. Топографы очень предусмотрительны, и, зная, что скорость может потребоваться для разных расчетов, они определяют ее во время съемки. Скорость течения выражают числом метров, преодолеваемых рекой за одну секунду, и подписывают на карте в разрыве стрелки, указывающей направление течения. Нужно знать еще поперечное сечение водного потока — то, что называют площадью живого сечения реки. Для определения этой величины воспользуемся другими числовыми данными — шириной и глубиной реки. Их подписывают на карте в виде дроби, в числителе которой указана ширина, а в знаменателе — глубина реки в метрах. Все необходимые данные у нас имеются.

Прежде всего определим площадь живого сечения каждой реки. Нам известно, что все реки, как правило, имеют постепенное увеличение глубины. Для приближенных расчетов можно считать, что указанная на карте глубина проходит не по всему участку поперечного сечения, а только по половине его. Таким образом, живое сечение реки имеет форму трапеции, площадь которой, как известно, равна произведению полусуммы оснований на высоту. Для реки Шуя трапеция имеет основания 40 и 20 м, и высоту 1,5 м, следовательно ее площадь составит [(40+20)/2]1,5 = 45 м². Для реки Сан размеры трапеции равны соответственно 60, 30 и 1,0 м; площадь ее равна [(60+30)/2]1,0 = 45 м².

Такое количество воды проносилось бы в каждой реке ежесекундно, если бы скорость течения составляла 1 м/с. В нашем случае река Шуя имеет скорость течения 2 м/с, а река Сан — 0,5 м/с. Значит, расход воды за 1 с в реке Шуя составит 90 м³, а в реке Сан — всего 22,5 м³, т. е. в 4 раза меньше.

Очень много интересных задач можно решать и по горизонталям, которые отображают рельеф местности на топографических картах. Даже простой овал одной горизонтали с бергштрихом может рассказать о многом: о том, что это форма рельефа суши и что эта форма положительная, о ее ориентировке в пространстве, высоте над уровнем моря, очертаниях к размерах. Если дополнить этот простой рисунок одной-двумя горизонталями, проходящими на известной высоте, то это позволит определить по карте высоту и направление уже более крупной формы земной поверхности, крутизну и направление ее склонов, а также абсолютные высоты и относительные превышения любых точек местности в пределах площади, оконтуренной нижней горизонталью.

Горизонталь — это след сечения земной поверхности горизонтальной плоскостью. А если земную поверхность пересечь вертикальной плоскостью, то в результате получится профиль рельефа местности.

Профили можно строить не только по прямым линиям, но и по любым кривым, например по дорогам, как это показано на рис. 43, а.

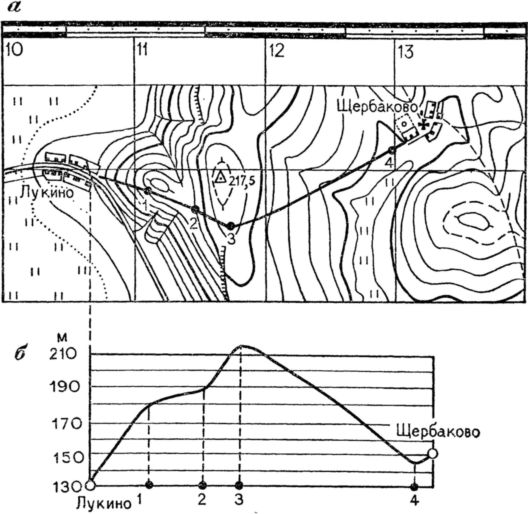
Рис. 43. Профиль рельефа вдоль дороги.

Для его построения на бумаге прочертим ряд параллельных линий, равных по длине протяженности дороги в масштабе карты (рис. 43, б). Расстояние между ними, соответствующее высоте сечения, берется равным 3–5 мм, а число линий равно числу горизонталей на данном участке, не считая равнозначных. Слева у параллельных линий подпишем отметки горизонталей, при этом меньшая по величине отметка должна быть внизу. Затем на карте по дороге наметим перегибы скатов (в нашем примере точки № 1, 2, 3, 4) и перенесем их на нижнюю линию. На исходном и конечном пунктах, а также на точках перегибов скатов определим по карте их абсолютные высоты. Они получились равными: окраина Лукино —130 м, № 1 — 180 м, № 2 — 190 м, № 3 — 212 м, № 4 — 145 м, окраина Щербакове — 150 м. От этих точек, перенесенных с карты на нижнюю линию чертежа, восставим перпендикуляры до пересечения с соответствующими по отметкам параллельными линиями. Точки пересечения соединим плавной линией и получим профиль нашего пути, который учитывает все неровности рельефа. В то же время он условный, так как вертикальные размеры на кем значительно больше, нежели полагалось бы по масштабу карты.

Если нужно представить вид земной поверхности с какой-либо точки, можно построить силуэт местности. Как это делается, видно на рис. 44.

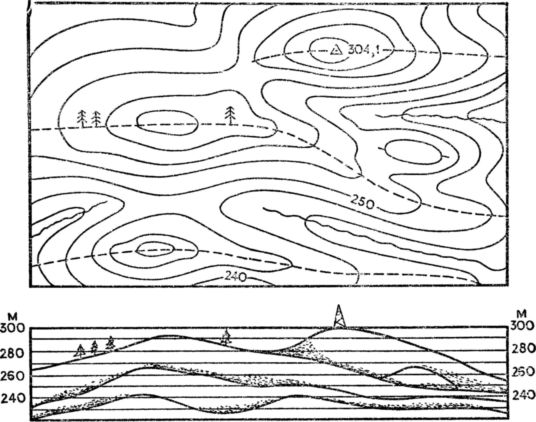
Рис. 44. Силуэт местности.

Вначале находят все водораздельные линии и на каждую из них строят профиль. Изображают при этом только те части профиля, которые не закрываются впереди лежащими возвышенностями.

Очень наглядно и вместе с тем достаточно точно рельеф какого-либо участка изображается на блок-диаграмме, которую нетрудно составить по топографической карте (рис. 45).

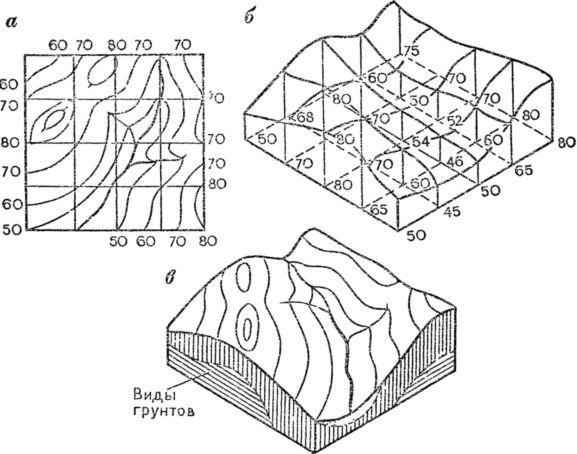
Рис. 45. Блок-диаграмма.

Блок-диаграмма — это трехмерный рисунок, совмещающий перспективное изображение поверхности и профили по двум взаимно перпендикулярным направлениям. Благодаря своей наглядности и трехмерности такие чертежи позволяют лучше представить взаимосвязи между явлениями, произвести измерения и сопоставления. По профильным плоскостям показывают обычно какую-либо геологическую структуру — виды грунтов, распределение вечной мерзлоты, грунтовых вод и др.

Блок-диаграмма строится в аксонометрической проекции, у которой оси располагаются под углом 120° друг к другу. Прежде всего трансформируем квадратную сетку топографической карты (рис. 45, а), направив ее стороны по горизонтальным аксонометрическим осям (рис. 45, б). Длины сторон при этом сохраняются неизменными. Затем у вершин каждой клетки выписываем абсолютные высоты, определенные по карте, и их значения в выбранном масштабе откладываем вдоль вертикальной оси. Соединив вершины отложенных отрезков, получим сетку квадратов в аксонометрической проекции. На эту сетку переносим с карты по клеткам горизонтали, реки и другие объекты. Подписи высот сотрем; на профильные грани нанесем геологические данные, и блок-диаграмма готова (рис. 45, в).

Масштабы вдоль боковых граней блок-диаграммы остаются теми же, что и на карте, а по вертикали масштаб равен масштабу профиля. Это позволяет проводить измерения на полученной модели в любых направлениях. Само же название «аксонометрия» означает «осеметрия», т. е. возможность вести измерения вдоль осей.

Если две поверхности, изображенные горизонталями на картах одного и того же масштаба, совместить, то можно произвести простейшие арифметические действия: слежение или вычитание рельефа поверхностей. При этом получится новая карта с изолиниями сумм или разностей. Задача сложения поверхностей может возникнуть, например, при подсчете мощности различных отложений. Вычитание одной поверхности из другой применяется при подсчете объема снесенного и отложенного материала, при определении поверхности стока воды и в других случаях.

Пусть требуется суммировать поверхности А и Б (рис. 46, а).

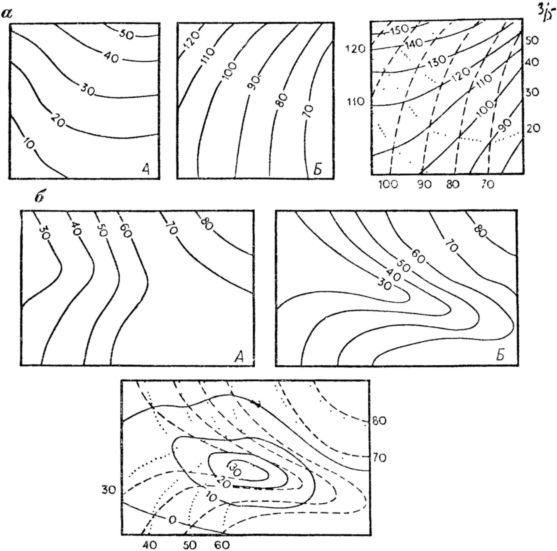
Рис. 46. Сложение и вычитание поверхностей.

Совместим обе карты. В точках пересечения изолиний определим суммы, и по ним проведем изолинии сумм А + Б. Легко заметить, что изолинии сумм обычно проходят по диагоналям четырехугольников, образованных пересекающимися изолиниями слагающих поверхностей. Это избавляет от обязательного суммирования значений в каждом пересечении и позволяет проводить изолинии сумм механически.

Графическое вычитание поверхностей рассмотрим на рис. 46, б. Здесь приведены два разновременных изображения одного и того же участка топографической поверхности. В первом случае А показана начальная стадия развития эрозионной формы, а во втором — Б — сформировавшаяся ложбина. Для подсчета объема снесенного грунта необходимо сперва получить разность поверхностей А — Б.

Как и в предыдущем примере, горизонтали совмещают на общей основе, а затем точки пересечения одноименных горизонталей соединяют плавной кривой. Получилась нулевая изолиния. Способ проведения остальных изолиний разности ясен из рисунка: он аналогичен проведению изолиний сумм. Получив карту разности, можно затем подсчитать объем снесенного грунта.

Рельеф, выраженный горизонталями, на первый взгляд не кажется наглядным. Но после небольшой тренировки в чтении рельефа карта перестает казаться нам плоским листом бумаги: она как бы приобретает третье измерение. Чтобы быстро ориентироваться в характере рельефа, сначала находят на карте наиболее низкие участки местности. Их легко обнаружить по расположению рек, озер, лугов, болот, песчаных отмелей и т. п. Затем постепенно от низин переходят к более высоким участкам. По виду горизонталей определяют лощины и хребты, а по густоте горизонталей выявляют характер склонов и их крутизну.