В.А. Фок
В.А. Фок
В нашем обсуждении квантовой механики упоминалось, что В.А. Фок был известным физиком-теоретиком, признанным во многих странах мира. В конце 50-х годов Фок утвердил себя как наиболее авторитетный интерпретатор отношения диалектического материализма к релятивистской физике. Он продолжал занимать это положение в 60-х и начале 70-х годов, несмотря на существование других советских интерпретаций. Хотя он умер в 1974 г., его интерпретация релятивистской физики оказывает воздействие в Советском Союзе и сегодня.
Фок неоднократно признавал, что он в долгу перед марксизмом как подходом к естествознанию. Во введении его книги «Теория пространства, времени и тяготения», изданной в 1955 г., Фок отмечал: «Общефилософская сторона наших взглядов на теорию пространства, времени и тяготения сложилась под влиянием философии диалектического материализма, в особенности же под влиянием книги Ленина „Материализм и эмпириокритицизм“»[920].
Такие заявления не были характерными для 50-х годов, равно как не являлись добавками к его научным работам. В 1966 г. в ответе по почте на вопрос американского журнала о его замечаниях по диалектическому материализму и естествознанию Фок писал: «Сущностью диалектического материализма является лишь комбинация диалектического подхода с принятием объективности внешнего мира. Без диалектического подхода материализм был бы сведен к механическому материализму, который был устаревшим даже в начале XX в. и является еще более устаревшим сейчас. С другой стороны, применение законов диалектики позволяет материалистической философии развиваться с прогрессом науки. Даже такие утверждения классического материализма, как полная независимость существования от возможности восприятия, могут быть переосмыслены и, при необходимости, пересмотрены без изменения сущности диалектического материализма. Способность этой формы философии идти в ногу с наукой является одной из ее характерных черт. Диалектический материализм является живой, а не догматической философией. Он помогает дать опыту, накопленному в одной области науки, настолько общую формулировку, что она может найти применение и в других областях».[921]
Фок выработал интерпретацию теории относительности, которая сохранила математическое ядро работы Эйнштейна, но приводила к некоторым новым понятиям. Фок отбросил термины «общая относительность», «общая теория относительности» и «общий принцип относительности». Вместо этого он называл теорию пространства Галилея[922] «теорией относительности» (а не «специальной теорией относительности») и теорию пространства-времени Эйнштейна «теорией тяготения» (а не «общей теорией относительности»).
Однако было бы большой ошибкой подчеркивать лишь фоковскую критику общей относительности. По сути дела, он рассматривал общую относительность (он бы сказал, теорию тяготения) как требовавшую интерпретационных разъяснений и методологических исправлений. В других отношениях он стойко защищал подход Эйнштейна, и, действительно, вполне возможно, что изначальная мотивировка Фока для написания работ по теории относительности и философии была защитной, то есть он стремился оградить теорию относительности от дискредитации в Советском Союзе. Но он обсуждал и защищал относительность в рамках диалектического материализма; есть серьезные основания полагать, что в ходе этого процесса он стал искренне интересоваться философскими проблемами естествознания. Его акцент на необходимости физического содержания в научных объяснениях — и не только математических форм — очевиден во многих его произведениях. Этот акцент был ясно связан с его материализмом.
Фок проводил четкие различия между физическими теориями в том виде, как они предстали в их завершенной форме, и методами, которыми они развивались. Фок полагал, что может иметь место принципиальное различие между начальными идеями, на базе которых была построена теория, и существенными идеями, которые она содержала после завершения[923]. Таким, по его мнению, был случай с общей относительностью. «Принцип относительности» (математически выраженный ковариантностью уравнений физики во всех системах отсчета) и «принцип эквивалентности» (математически выраженный идентичностью инерциальной и гравитационной масс) играли важную роль в мыслях Эйнштейна, когда он создал теорию общей относительности; но Фок был уверен, что эти принципы не лежали в основе относительности в физическом смысле. В действительности, согласно Фоку, принцип эквивалентности был лишь приблизительным утверждением, в то время как принцип относительности (общая ковариантность) вступал в противоречие с характеристиками существующего поля гравитации. Принципы эквивалентности и относительности могут быть получены из целостной структуры общей относительности в том виде, как ее представлял Эйнштейн, но, по словам Фока, они не были существенны для нее как для теории тяготения. Давайте рассмотрим его анализ более детально.
Ключом ко взгляду Фока на общую относительность (которую всегда необходимо отличать от специальной относительности, полностью принимавшейся Фоком) было его мнение о том, что Эйнштейну не удалось усмотреть важности пространства-времени «как целого» и что он вместо этого уделял внимание локальным областям внутри пространственно-временного континуума. Этот акцент привел к тому, что Эйнштейн, по словам Фока, не придал значения тому факту, что его ОТО вовсе не является обобщением СТО, а, наоборот, является ее ограничением. Вместо того чтобы обобщить понятие относительности, Эйнштейн, по словам Фока, обобщил просто определенные геометрические понятия, изменив одновременно своей первоначальной релятивизации пространства и времени.
Фок начал свое обсуждение теории относительности с замечания о том, что теория пространства и времени может быть разделена на две части: теорию однородного (галилеевского) пространства и теорию неоднородного (римановского, эйнштейновского) пространства. Первая половина занимала внимание Эйнштейна в ходе его развития СТО, а затем он попытался (неудачно, по словам Фока) обобщить свою теорию в ОТО.
Основной характеристикой галилеевского пространства выступает его однородность, которая может быть проиллюстрирована эквивалентностью всех пунктов, направлений и инерциальных систем внутри него. Как ньютоновская физика, так и физика СТО были основаны на допущении однородного (галилеевского) пространства. Математически однородность пространства в физике Ньютона была выражена в преобразованиях Галилея; однородность пространства СТО была выражена в преобразованиях Лоренца. Лишь в переходе от СТО к ОТО допущение галилеевского пространства было отброшено и, по словам Фока, на очень правильных основаниях.
Эйнштейн правильно показал, продолжал Фок, что универсальная теория гравитации (ОТО) не может содержаться в рамках галилеевского пространства. Наиболее существенной причиной неадекватности галилеевского пространства, по словам Фока, была та, которую дал Эйнштейн: не только инертная масса тела, но и его гравитационная масса зависит от его энергии. Эйнштейн нашел способ описания новой физики посредством математического замещения галилеевского пространства на пространство Римана. Таким образом, он создал то, что обычно называют общей теорией относительности, новую физическую теорию. Но, согласно Фоку, новая теория, являясь необычайно ценной как теория гравитации, вовсе не была физической теорией общей относительности. Позже Фок сформулировал свою критику в форме, которую он назвал «двумя короткими фразами»: 1) физическая относительность не есть общая; 2) общая относительность не есть физическая[924]. Позиция Фока серьезно рассматривалась многими советскими и зарубежными естествоиспытателями. Обсуждение ее продолжается и сегодня.
Что же Фок считал концептуальной ошибкой Эйнштейна? Корень этого может быть найден в эйнштейновском понимании и использовании принципа эквивалентности, согласно которому в бесконечно малой области гравитационное поле эквивалентно ускорению. Эйнштейн иллюстрировал это с помощью известного мысленного эксперимента: если масса m прикреплена на пружине к потолку кабины (лифта) следующим образом:
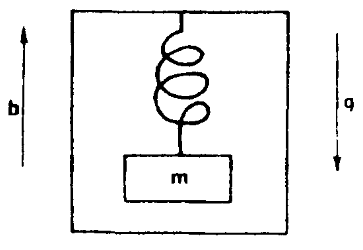
тогда, находясь внутри лифта, невозможно сказать, вызвано ли растяжение пружины направленным вверх ускорением лифта в направлении b или направленным вниз гравитационным полем в направлении g[925]. Более обычной иллюстрацией является то, что пилот самолета при «слепом» полете в облаке не может отличить, чем вызвано вдавливание его в кресло: гравитацией или же полетом в мертвой петле, сходство которых теперь алгебраически демонстрируется описанием обеих сил в терминах g.
Эйнштейн так графически объяснял свой принцип эквивалентности, который может быть просто сформулирован как принцип эквивалентности инертной и гравитационной масс. Эйнштейн перешел далее к приложению этого представления к земному тяготению. На первый взгляд это кажется невозможным, так как любое ускорение, двигающее Землю в целом, будет иметь весьма различные эффекты в различных районах поверхности планеты. Однако гравитационные силы могут быть «устранены преобразованием», если мы рассмотрим лишь бесконечно малые области, описываемые с помощью дифференциальных уравнений. Так, если мы представим сеть клеток, наложенную на Землю, где каждая клетка представляет бесконечно малую область, в следующем виде:
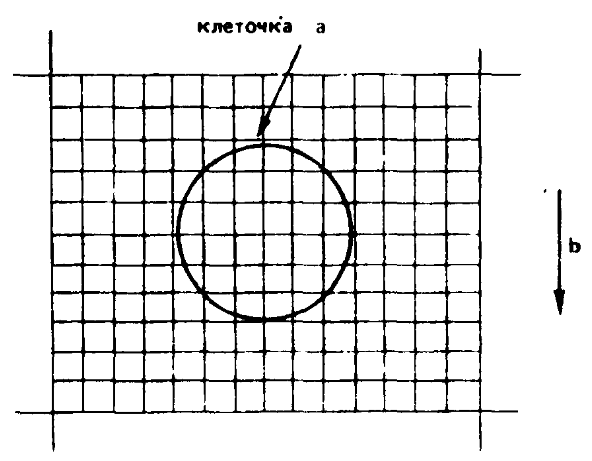
то становится явным, что сила гравитации в любой точке поверхности Земли может быть «устранена преобразованием», с помощью воображаемого соответствующего ускоренного перемещения сетки. Если мы позволим этой системе двигаться с ускорением 9,8 м/сек2 в направлении b, то гравитационное поле в клеточке а исчезнет так же, как сила тяжести исчезает в свободно падающем лифте[926].
Вышеприведенные примеры принципа эквивалентности помогают понять, что, согласно эйнштейновской теории гравитации, в любой данной точке пространства гравитационное поле можно заменить соответствующим ускорением. Это же отношение передается наблюдением, что, хотя пространство Эйнштейна в целом неоднородно, в любой бесконечно малой области оно однородно и преобразования Лоренца имеют силу.
Именно в этом пункте Фок расходился со взглядом Эйнштейна. Он утверждал, что локальная эквивалентность ускорения и гравитации не была достаточным основанием для вывода о полной эквивалентности полей ускорения и гравитации во всем пространстве. В действительности, Фок рассматривал принцип эквивалентности имеющим силу лишь в ограниченном, локальном смысле. Согласно Фоку, принцип эквивалентности в законченной теории Эйнштейна имел «приближенный характер и не является общим принципом»[927].
Фок отмечал, что физическим базисом принципа эквивалентности является закон падающих тел, согласно которому все свободно падающие тела двигаются равноускоренно. Но этот закон является общим законом, отмечал Фок, а не локальным, и если его использовать для обоснования другого общего закона (относительности), то должен быть найден некоторый способ рассмотрения пространства как целого. «При построении теории тяготения нельзя ограничиться локальным рассмотрением (т. е. рассмотрением бесконечно малых областей пространства). Необходимо так или иначе характеризовать свойства пространства в целом; в противном случае вообще нельзя поставить задачу однозначным образом, Это особенно ясно из того факта, что уравнения всякого поля (также и поля тяготения) представляют уравнения в частных производных, решения которых получаются однозначно лишь при наличии начальных и предельных условий или условий, их заменяющих. Уравнения поля и предельные условия неразрывно связаны друг с другом, и последние никак нельзя считать чем-то менее важным, чем сами уравнения. Но в задачах, относящихся ко всему пространству, предельные условия относятся к отдаленным областям пространства и для их формулировки необходимо знать свойства пространства в целом.
Заметим, что недостаточность локального рассмотрения и важность предельных условий были явно недооценены Эйнштейном, в связи с чем в наших работах и в настоящей книге нам пришлось внести в постановку основных задач теории тяготения существенные изменения»[928].
Фок характеризовал предельные условия двояко. В первом случае он допускал однородность пространства на бесконечности, в смысле описания преобразованиями Лоренца. Массы и связанные с ними гравитационные поля в таком случае были представлены как имплантированные в однородное галилеевское пространство (отметим, не в конечное, а в неограниченное пространство-время). Второй случай предполагал пространство-время, которое лишь частично однородно и пространственная часть которого подчиняется геометрии Лобачевского. Обычно называемое пространством Фридмана — Лобачевского, оно содержит хорошо определенные гравитационные поля, когда средняя плотность материи, содержащаяся внутри него, не равна нулю.
Важные выводы из этих соображений и других, которые наиболее ярко показывают неортодоксальность позиции Фока, связаны с вопросом о привилегированных системах координат. В каждом из рассмотренных Фоком типов пространств — то есть в галилеевском пространстве, пространстве однородном на бесконечности и пространстве Фридмана — Лобачевского, — «возможно», имеется, согласно Фоку, «привилегированная система координат»[929]. Слово «возможно» указывает на сохраняющиеся сомнения Фока относительно пространства Фридмана — Лобачевского. В случае с галилеевским пространством и пространством однородным на бесконечности он был уверен в существовании привилегированной системы координат. Существование таких привилегированных систем координат в каждом случае было бы, конечно, противоречащим эйнштейновской концепции полной релятивизации движения. Точно так же как СТО ассоциируется с релятивизацией инерциального движения (и, таким образом, с эквивалентностью инерциальных систем отсчета), так ОТО ассоциируется с релятивизацией ускоренного движения (и следовательно, эквивалентностью ускоренных систем отсчета). Но теперь Фок ставил под вопрос возможность рассматривать ОТО как реальное обобщение СТО в этом смысле.
Фок посвятил большую часть своего исследования задаче доказательства, что в однородном на бесконечности пространстве существует привилегированная система координат, которая хорошо определяется без преобразований Лоренца. Он думал, что такая система формируется гармоническими координатами, которые, по мнению Фока, отражали внутренние свойства пространства-времени[930]. Однако необходимо отметить, что вера в гармонические координаты была одним из наиболее спорных аспектов его подхода; несколько физиков, принявших его критику концепции общей относительности, сомневались в привилегированном статусе гармонических координат[931]. Фок признал эту критику в своем заявлении: «Сделанные выше замечания о привилегированном характере гармонической системы координат ни в коем случае не должны быть понимаемы в смысле какого-либо запрещения пользоваться другими координатными системами. Ничто не может быть более чуждым нашей точке зрения, чем такое ее толкование… Существование гармонических координат, хотя и является фактом первостепенного теоретического и практического значения, но никоим образом не исключает возможности пользоваться другими, негармоническими, координатными системами»[932].
Фок верил, что многие физики упустили из виду важность предпочтительных или привилегированных систем координат в результате преувеличения ими значения ковариантности уравнений и особенно их уверенности, что эта ковариантность отражает определенный тип физического закона. Например, используя понятия тензорного анализа, физики могли записать уравнения для пространственно-временных интервалов, не предполагая заранее каких-либо координатных систем[933]. Такие уравнения очень удобны, так как они позволяют существенно экономить в математическом описании пространства-времени. Однако, писал Фок, значение таких ковариантных выражений физических фактов в том, что не все координатные системы (в природе) действительно равны. Указанием на эту основную бессодержательность (с физической точки зрения, что всегда подчеркивал Фок) ковариантности является тот факт, что практически любое уравнение может быть задано в ковариантной форме, если ввести достаточное количество дополнительных функций[934]. В ковариантном выражении бесконечно малых пространственно-временных интервалов вводимая дополнительная функция есть коэффициент G?? являющийся тензором. Важным фактом является то, что эта введенная функция G?? есть единственная функция, используемая для описания гравитационного поля. Но надо заметить, писал Фок, что в этом процессе происходит введение подходящей теории гравитации в теорию, которая, таким образом, неподходяще дублирует ОТО, как будто результаты были дальнейшим выражением относительности движения. Как отмечал Фок, «между тем с созданием теории тяготения Эйнштейна вошел в употребление термин „общая относительность“, который все запутал. Термин этот стал применяться в смысле „общей ковариантности“ (т. е. в смысле ковариантности уравнений по отношению к произвольным преобразованиям координат, сопровождаемым изменением вида функции G??). Но мы видели, что такая ковариантность… ничего не имеет общего с „относительностью просто“. Между тем эта последняя получила название „частной“, которое как бы указывает, что она является частным случаем „общей“…
Термин „общая относительность“ или „общий принцип относительности“ употребляется (прежде всего самим Эйнштейном) еще и в смысле условного наименования для теории тяготения. Уже основная работа Эйнштейна по теории тяготения (1916 г.) озаглавлена „Основы общей теории относительности“. Это еще больше запутывает дело… Так, поскольку в теории тяготения пространство предполагается неоднородным, а относительность связана с однородностью, то выходит, что в общей теории относительности нет, вообще говоря, никакой относительности»[935].
Среди ведущих физиков не существует согласия по поводу фоковской критики «общей относительности». Интерпретация Фока подвергалась обсуждению и в Советском Союзе, и за рубежом. До сих пор она продолжает вызывать уважение и внимание как хорошо обоснованная и интересная точка зрения. В 1964 г. Фок представил во Флоренции (Италия) доклад, в котором он сжато изложил вышеупомянутый анализ для аудитории известных ученых. В последующей дискуссии отдельные аспекты фоковской схемы получили определенное признание, в то время как другие были признаны более спорными. Герман Бонди, профессор прикладной математики из Кингз колледжа Лондонского университета, соглашался с фоковской критикой утверждения физической эквивалентности между инерциальными и ускоренными наблюдателями[936]. Профессор Андре Лихнерович из Коллеж де Франс также поддерживал фоковскую критику принципа эквивалентности, а Стэнли Дезер из Университета Брандайза отмечал, что фоковский анализ понятия ковариантности был очень полезным для его более полного понимания общей относительности[937]. Но некоторые из присутствующих ученых, включая Лихнеровича и Дезера, были менее воодушевлены использованием Фоком гармонических координат. Определенное число физиков-теоретиков не верило, что гармонические координаты подходят для описания гравитационного поля, как на то указывал Фок.
К концу 60-х годов в Советском Союзе появилось множество различных типов интерпретации общей относительности. Фоковская интерпретация была одной из них, хотя, вероятно, наиболее распространенной. П. С. Дышлевый писал в 1969 г., что советских философов и естествоиспытателей можно условно разделить на три группы в зависимости от их отношения к общей относительности[938]. Первую группу составляли исследователи, считавшие ОТО Эйнштейна, по существу, завершенной теорией. Они вводили отдельные модификации, но в целом они полностью принимали эйнштейновскую интерпретацию относительности, полагая, что она не представляет серьезных философских или естественнонаучных проблем. Они рассматривали критицизм Фока (Фок не входил в эту группу) по отношению к общей относительности как слишком неортодоксальный в терминологическом и концептуальном планах. Эти ученые принимали использование термина «общая теория относительности» (в противоположность Фоку) и были не столь критически настроены к эйнштейновскому использованию принципа эквивалентности. Они были, в общем, скептически настроены к попыткам добавить «третью ступень относительности», такую, как «единая теория поля». Эти ученые хотели принять современное здание теории относительности с его двумя этажами: СТО и ОТО. Среди советских ученых, которых Дышлевый зачислил в эту группу, были в прошлом — М. Бронштейн, Я. Френкель, А. Фридман, В. Фредерикс, в конце 60-х годов — А.Ф. Богородский, В.Л. Гинзбург, Я.Б. Зельдович, X.П. Керес, А.С. Компанеец и М.Ф. Широков.
Лидером второй группы интерпретаторов общей относительности в Советском Союзе был Фок. Основное утверждение этой группы сводилось к положению, что основания общей относительности должны быть полностью пересмотрены, для того чтобы исправить концептуальную структуру той теории, которая была представлена Эйнштейном[939]. Я уже рассматривал взгляды этой группы в деталях в ходе обсуждения представлений Фока. Другими естествоиспытателями, которых Дышлевый относил к этой группе, были А.3. Петров и Н.В. Мицкевич.
Третья группа советских интерпретаторов теории относительности надеялась достичь новой формулировки общей относительности посредством объединения квантовой и релятивистской физики в новую квантовую теорию гравитации. Ее представители подходили к гравитации с точки зрения теории поля, которая была разработана в отношении физических полей, отличных от гравитационного. Дышлевый назвал следующих членов этой группы: Д.Д. Иваненко, О.С. Иваницкая, М.М. Мирианашвили, В.С. Кирия, А.Б. Кереселидзе, А.Е. Левашев и В.И. Родичев.
Из этих групп лишь вторая призывала к специфическим изменениям в интерпретациях общей относительности. Первая группа принимала общую относительность в виде, очень близком к ее существующей форме, в особенности те философские традиционные интерпретации ее, которые укладывались в рамки материалистических традиций. Третья группа предлагала программу на будущее, которая, при условии ее успеха, несомненно, имела бы философские последствия, но которая до этих пор обсуждалась только в начальных формах. Вторая группа, однако, продолжала выдвигать критику, изначально формулировавшуюся Фоком. Именно эта группа и ее комментаторы выработали большую часть философской литературы по теории относительности.
Действительно, многие из членов первой и третьей групп избегали философских вопросов естествознания. За исключением М. Ф. Широкова (первая группа) и Д. Д. Иваненко (третья группа), их фамилии лишь редко появлялись в библиографиях статей и книг по диалектическому материализму[940]. Из названных двух ученых М. Ф. Широков был тем, чьи идеи наиболее прямо вторгались в обсуждение общей относительности.
Широков признавал значение термина «общая относительность» и этим выступал против критики второй группы и делал это в отличие от некоторых его коллег — явно в рамках диалектического материализма. Он утверждал, что эйнштейновская интерпретация относительности полностью созвучна с диалектическим материализмом и, по сути дела, является его дальнейшим подтверждением. В 1964 г. он писал об общей относительности: «Эта теория… является также большим достижением в материалистическом понимании природы, вопреки многочисленным идеалистическим (особенно в духе махизма) толкованиям ее некоторыми зарубежными авторами»[941]. Широков полагал, что Фок и Александров недооценивали ОТО и сильно упрощали ее значение сведением к теории гравитации. Однако он признавал важность их работ в «подтверждении», что теория относительности отражает «объективность и реальность» природы. Их ошибкой была неспособность усмотреть тот факт, что, отрицая ОТО, они также отрицали объективную реальность полей инерциальных сил[942]. Широков, как и Фок, однако, придерживался идеи о привилегированной системе отсчета в ОТО, основываясь на собственном представлении о понятии «центр инерции». В этом смысле он соглашался с Фоком в выдвижении причин для предпочтения коперниковского взгляда (по сравнению с птолемеевским), но если Фок основывал свою аргументацию на своих гармонических координатах пространства, однородного на бесконечности, то Широков указывал, что Солнце представляет подходящий центр инерции для Солнечной системы[943].
Один вопрос, связанный с общей относительностью, представлял собой основу больших разногласий среди естествоиспытателей и философов в Советском Союзе: «Что есть гравитация?» На него давались самые различные ответы[944]. Члены первой группы часто приравнивали гравитационное поле к искривленному пространству-времени. Однако некоторые из их критиков утверждали, что этот ответ подразумевает почти лишение гравитации физического или материального содержания, отождествление природы с геометрией, то есть позиции, которой марксисты традиционно противостояли. М. Ф. Широков, член первой группы, из-за этого определил свою позицию очень тщательно. Согласно ему, гравитация «отражает геометрические свойства пространства-времени»; гравитационное поле не обладает массой или энергией; гравитация не есть, таким образом, сама материя, а есть вместо этого «форма существования материи». Д.Д. Иваненко определял гравитацию несколько иначе; она была для него искривлением пространства-времени, вызванным материей и самим гравитационным полем. Так, гравитация была, по Иваненко, не совсем тем же, что пространство-время, но вместо того была независимым аспектом материального мира. А.З. Петров, член второй группы, описывал гравитационное поле как «специфическую форму движущейся материи». Н.В. Мицкевич разделял эту позицию и предупреждал против сведения гравитации к геометрии. По его мнению, скорее геометрия есть выражение гравитационного поля, а не наоборот. Таким образом, существовало известное различие взглядов среди советских ученых. Попытка определить «гравитацию» была в Советском Союзе объектом дискуссии, в некоторой степени очень сходной с попытками определить «информацию» и «сознание» в других дисциплинах. Последние термины обсуждались в других главах.
К середине 80-х годов философские проблемы теории относительности казались менее проблематичными советским философам физики, чем вопросы квантовой механики. Тем не менее, значительная работа в этой области была проделана за последние пятнадцать лет, особенно над творческим наследием Эйнштейна, который теперь является объектом поклонения советских интеллектуалов[945]. Важной проблемой в теории относительности, которая привлекла внимание, была возможность существования частиц, движущихся со сверхсветовыми скоростями, названных «тахионами» американским физиком Дж. Файнбергом. Центром советской дискуссии был вопрос: «Может ли математика специальной теории относительности служить теоретической базой для описания частиц со сверхсветовыми скоростями, и если да, то не ведет ли это к отрицанию причинности?» Большинство советских физиков и философов, писавших по этому предмету, кажется, стремились дать на этот вопрос положительный ответ, но некоторые выражали опасения относительно высокой философской цены такого признания и поэтому советовали соблюдать осторожность[946]. Советские философы даже в 80-х годах признавали, что этот вопрос был как методологическим, так и «мировоззренческим»[947]. Советским марксистам удалось перейти от жесткой причинности к вероятностной причинности перед лицом развития физики, вопрос о полном отказе от причинности лежал в иной плоскости и был значительно более принципиальным.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК