5.2. Как появились арабские цифры для позиционной записи чисел?
5.2. Как появились арабские цифры для позиционной записи чисел?
Д.Л. Стройк пишет: «Весьма разнообразны знаки, которые применялись для записи цифр в позиционной системе, но имеются два главных типа: индийские обозначения, которые применялись восточными арабами, и так называемые цифры „гобар“ (или „губар“), которые применялись западными арабами в Испании. Знаки первого типа и сейчас еще применяются в арабском мире, но наша современная система, по-видимому, произошла из системы „гобар“» [821], с. 89.
ВОПРОС О ПРОИСХОЖДЕНИИ «АРАБСКИХ ЦИФР» ОСТАЕТСЯ В СКАЛИГЕРОВСКОЙ ИСТОРИИ НАУКИ ОТКРЫТЫМ ДО СИХ ПОР. Существуют различные теории на этот счет. Например, теория Вепке, согласно которой арабские цифры проникли на Запад якобы в V веке из Александрии через неопифагорейцев [821], с. 90. Есть и другая теория — Н.М. Бубнова. Согласно ей, знаки «гобар» произошли из давних римско-греческих символов [821], с. 90. Но ни в том, ни в другом случае не предъявляются РОДОНАЧАЛЬНИКИ хорошо знакомых нам арабских цифр. В качестве таких родоначальников являются ЗАБЫТЫЕ римско-греческие или александрийский символы. Сегодня неизвестные.
Известный русский историк математики В.В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕЕ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метод внушения, впечатление КАК БЫ ЧЕГО-ТО ДОКАЗАННОГО». Цит. по [989], с. 53. Авторы Энциклопедии [989], после изложения различных теорий происхождения арабских цифр делами следующий многозначительный вывод: «Таким образом, МЫ ДО СИХ ПОР НЕ ИМЕЕМ ИСТОРИЧЕСКИ ОБОСНОВАННОЙ ГИПОТЕЗЫ, КОТОРАЯ ДОСТАТОЧНО УДОВЛЕТВОРИТЕЛЬНО ОБЪЯСНЯЛА БЫ ПРОИСХОЖДЕНИЕ НАШИХ ЦИФР» [989], с. 52.
Нам представляется, что дело не такое уж и сложно. Стоит лишь отрешиться от неправильных скалигеровских датировок, как происхождение «арабских цифр» становится почти очевидным. И весьма естественным. Как мы сейчас покажем, ВСЕ «АРАБСКИЕ ЦИФРЫ» ПРОИЗОШЛИ ИЗ ПРЕДШЕСТВУЮЩЕЙ ПОЛУ-ПОЗИЦИОННОЙ СЛАВЯНО-ГРЕЧЕСКОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем ясно будет видно, что был использован именно СЛАВЯНСКИЙ ВАРИАНТ букв-символов. Источником послужила русская скоропись XVI века. ПРОИЗОШЛО ВСЕ ЭТО, СКОРЕЕ ВСЕГО, В XVI ВЕКЕ. То есть как раз в эпоху изобретения нуля и позиционной системы счисления. Перейдем к подробному изложению.
До изобретения позиционной системы счисления и арабских цифр на Руси использовалась полу-позиционная система, где для каждой десятичной цифры имелось три различных знака, в качестве которых выступали церковно-славянские буквы кириллицы [782], вып. 1, с. 16. Одна буква предназначалась для изображения данной цифры в разряде единиц. Другая — для изображения той же цифры в разряде десятков. И наконец, третья — в разряде сотен, рис. 62. Ноль отсутствовал, но, поскольку в разных разрядах обозначение цифр было разным само обозначение цифры указывало на разряд, в котором она стоит. С помощью такой системы можно было производить все обычные арифметические действия с целыми числами в пределах от единицы до тысячи. Для чисел больше тысячи приходилось применять специальные дополнительные значки, рис. 62.
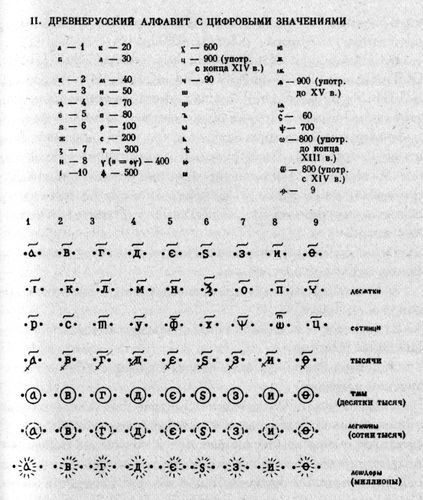
Рис. 62. Старая славяно-греческая полу-позиционная система записи цифр. Взято из [782], вып. 1, с. 16.
Поясним таблицу на рис. 62. Например, цифра «один» изображалась тремя способами:
1) буквой А, если единица стояла в разряде единиц, то ее в первом разряде;
2) буквой I, если единица стояла в разряде десятков, то есть во втором разряде;
3) буквой Р, если единица стояла в разряде сотен, то есть в третьем разряде.
Скажем, число РА означало 101. В нынешней позиционной системе при записи числа 101 используется ноль, так как отсутствует цифра во втором разряде. В старой же славянской полу-позиционной записи нуля не было, но само обозначение единицы разными буквами указывало, что последняя из них стоит в первом, а первая — в третьем разряде. Таким образом, для записи целых чисел от единицы до тысячи использовалось не ДЕСЯТЬ символов, как сегодня — ДЕВЯТЬ ЗНАЧАЩИХ ЦИФР И НОЛЬ, — а ДВАДЦАТЬ СЕМЬ букв кириллицы. НА КАЖДУЮ ЗНАЧАЩУЮ ЦИФРУ ПРИХОДИЛОСЬ ТЕМ САМЫМ ПО ТРИ БУКВЫ. В таблице на рис. 62 двадцать семь кириллических букв расположены в трех верхних строках. Под каждой арабской цифрой мы видим три различные буквы кириллицы. Остальные четыре строки таблицы на самом деле повторяют первую строку, но снабжены специальными дополнительными символами, чтобы обеспечить следующие разряды от тысячи до миллиона. Новые буквы при этом не используются.
Зададимся вопросом. Что должно было произойти, когда указанную старинную систему обозначений решили заменить на нынешнюю позиционную систему с нулем? Для этого нужно было оставить вместо двадцати семи знаков всего лишь девять (и добавить ноль). Самый простой и естественный способ — оставить из трех обозначений-букв для каждой цифры только одну кириллическую букву.
Оказывается, именно это и было сделано. Как мы сейчас увидим, в результате получились привычные нам сегодня «арабские цифры». Что сразу же делает очевидным тот факт, что люди, впервые придумавшие «арабские цифры», пользовались до этого именно славяно-греческой полу-позиционной системой счисления. Причем для «арабских цифр» были использованы во многих случаях именно РУССКИЕ СКОРОПИСНЫЕ формы XVI века кириллических букв. Что может означать лишь одно. Для изобретателей арабских цифр русская СКОРОПИСЬ XVI ВЕКА была хорошо знакомым, привычным почерком.
В частности, исчезает и «великая загадка» скалигеровской истории — откуда же взялись «арабские цифры»? Они произошли из славяно-греческих цифр-букв в формах русской скорописи XVI века. Кроме того, и другие детали, о которых мы ниже расскажем, однозначно показывают, что использовалась именно РУССКАЯ, а не ГРЕЧЕСКАЯ азбука XVI века. Эти азбуки несколько отличаются.
Обратимся теперь к таблице на рис. 63. Обсудим каждую Цифру отдельно.
ЕДИНИЦА. Из трех возможных обозначений единицы была выбрана буква I (единица в разряде десятков) как наиболее простая из трех. Она обведена кружком на рис. 63. Получилась «индо-арабская» единица.
ДВОЙКА. Для двойки была использована не буква В (то есть вторая буква греческой азбуки), а буква Б — вторая буква ЦЕРКОВНО-СЛАВЯНСКОЙ азбуки. При этом была взята скорописная форма этой буквы, перевернута и зеркально отражена, рис. 63. Получилась привычная нам сегодня «индо-арабская» двойка. В данном случае автор новых обозначений явно доказал свое предпочтение славянской азбуке перед греческой, в греческой азбуке буквы Б нет. Она пропущена, и сразу после А идет В.
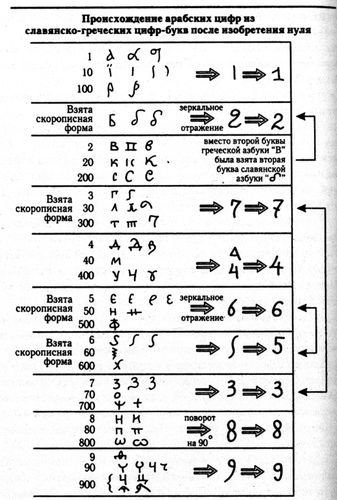
Рис. 63. Наша схема происхождения арабских цифр из славянских цифр-букв предшествующей полу-позиционной системы счисления. Обратите внимание, что во многих случаях ДЛЯ АРАБСКИХ ЦИФР БЫЛИ ВЗЯТЫ РУССКИЕ СКОРОПИСНЫЕ ФОРМЫ КИРИЛЛИЧЕСКИХ БУКВ.
Тройку мы пока пропустим, так как ее обозначение переставлено с семеркой.
ЧЕТВЕРКА. У четверки есть две формы: открытая и закрытая. Закрытая форма «домиком» получается из славянской буквы Д, обозначавшей четверку в первом разряде. Открытая же форма получается из славянской буквы У, обозначавшей четверку в третьем разряде, рис. 63. Получилась «индо-арабская» четверка.
Пятерку, шестерку и семерку мы пока пропустим, так как их обозначения переставлены. Подробнее об этом ниже.
ВОСЬМЕРКА. Она получается из славянской буквы «омега», обозначавшей восьмерку в третьем разряде. Буква повернута на девяносто градусов, рис. 63. Получилась «индо-арабская» восьмерка.
ДЕВЯТКА. Здесь для «индо-арабской» цифры была использована нестандартная, ЧИСТО РУССКАЯ форма девятки в третьем разряде. Обычно в славяно-греческих обозначениях для этого использовалась буква Ц. Однако на Руси использовали также букву Я для обозначения девятки в третьем разряде. Мы видим, что ее скорописная форма — это в точности «индо-арабская» девятка с приделанной палочкой. Палочку отбросили. Получилась хорошо знакомая нам сегодня «индо-арабская» цифра девять, рис. 63. Упомянутая скорописная форма буквы Я была с небольшими изменениями канонизирована во время Петровской реформы и используется до сих пор. На рис. 64 приведен образец Русской скорописи начала XVII века [791], вып. 19, форзац. Здесь написано русское слово «знамя». В его конце стоит буква Я.
Перейдем теперь к «индо-арабским» цифрам: ТРОЙКА, Пятерка, шестерка и семерка.
Рис. 64. Скорописная форма славянской буквы Я в конце слова «знамя». Ясно видно, что если отбросить верхнюю палочку, то получится «ИНДО-АРАБСКАЯ» ДЕВЯТКА. Взято из [791], вып. 19.
Рис. 65. Скорописная форма славянской буквы Т в начале слова. Ясно видно, что это в точности «ИНДО-АРАБСКАЯ» СЕМЁРКА. Взято из [791], вып. 19.
ТРОЙКА и СЕМЁРКА. Для «индо-арабской» тройки была использована русская скорописная форма буквы 3, обозначавшая семерку в первом разряде, рис. 63. Формы русской скорописной буквы 3 и «индо-арабской» тройки полностью идентичны. И наоборот, для «индоевропейской» семерки была использована скорописная форма русской буквы Т, обозначающая тройку в третьем разряде, рис. 65. Таким образом, обозначения для тройки и семерки были почему-то ПЕРЕСТАВЛЕНЫ местами.
ПЯТЕРКА и ШЕСТЕРКА. Для «индо-арабской» пятерке была использована скорописная форма русской буквы «зело», обозначавшая шестерку в первом разряде, рис. 63. И наоборот для «индо-арабской» шестерки была использована скорописная форма славянской буквы Е, обозначавшей пятерку в первом разряде. Эта форма, кстати, очень близка к современна форме рукописной буквы Е. Создатели «индо-арабских» цифр просто зеркально отразили славянскую букву Е и получили шестерку. На рис. 66 приведен образец русской скорописи начала XVII века, где буква Е в конце слова «великие» написан как зеркально отраженная шестерка [787], вып. 7. Таким образом, обозначения для пятерки и шестерки были почему-то ПЕРЕСТАВЛЕНЫ местами. Как и в случае тройки и семерки.
Рис. 66. Скорописная форма славянской буквы Е в конце слова «великие». Ясно видно, что это в точности «ИНДО-АРАБСКАЯ» ШЕСТЕРКА получается из этой буквы Е зеркальным отражением. Взято из [787], вып. 7.
НОЛЬ. Вопрос о НУЛЕ особенно интересен. Поскольку именно изобретение нуля позволило ввести НОВУЮ СИСТЕМУ СЧИСЛЕНИЯ. В современной системе счисления ноль обозначает место ОТСУТСТВУЮЩЕЙ ЦИФРЫ в том или ином разряде. Вместо нее ставится ноль. Зададимся вопросом: откуда произошло обозначения нуля привычным ныне кружочком? Старые обозначения обычно не были совсем отвлеченными, поэтому, скорее всего, обозначение нуля явилось сокращением (или видоизменением) какого-то осмысленного слова. Зададимся вопросом: какого именно? Оказывается, это легко и естественно объясняется в предположении, что исходное слово было славянским. Как сообщает В.И. Даль, слово или предлог О в русском языке раньше могло употребляться вместо приставки ОТ [223], т. 2, столбец 1467. Приставка же ОТ означает ОТСУТСТВИЕ. Этимологический словарь: ОТ — «глагольная приставка — обозначает прекращение, завершение действия; удаление, устранение чего-либо» [955], т. 1, с. 610. Таким образом, отсутствующую цифру вполне естественно было обозначить символом, похожим на букву О. По-видимому, именно так и возник современный знак нуля — кружочек «0». Что касается самого слова НОЛЬ, то оно могло произойти от старого русского НОЛИ или НОЛЬНО. Сегодня это слово уже забыто, но раньше оно часто использовалось в русском языке. Об этом говорят многочисленные примеры его употребления в старых текстах, приведенные в Словаре русского языка XI–XVII веков [789], с. 420–421. Слово НОЛЬНО, или НОЛЬНЫ, НОЛЬНЕ, НОЛЬНА использовалось, в частности, как ограничительная частица, в смысле «не прежде чем, только когда» [789], с. 421. Но ведь и ноль в десятичной записи числа можно рассматривать, как ограничительный знак, «не пускающий» цифру соседнего разряда на место отсутствующей цифры данного разряда. Дело в том, что в предшествующей славяно-греческой полу-позиционной системе счисления при отсутствии значащей цифры в том или ином разряде цифры соседних разрядов придвигались друг к другу, занимая пустые места отсутствующей цифры. Именно поэтому приходилось обозначать одни и те же цифры в разных разрядах разными буквами — чтобы различить их. В позиционной же системе не нужно, поскольку на место отсутствующей значащей цифры другие цифры попасть не могут — их «не пускает» ноль. Итак, ноль могли первое время рассматривать как «не пускающий» знак, а значит, и его название вполне могло произойти от ограничительной частицы НОЛЬНО в старом русском языке. Нольно — ноль.
Кроме того, слово НОЛИ в старом русском языке употреблялось также и для обозначения не осуществившейся возможности: «помышлялъ есмь въ себе:… ноли буду лучии тогда, но худъ есмь и боленъ» [789], с. 420. В современном переводе: думал про себя: может быть, («ноли») буду лучше тогда, [но это не осуществилось], я плох и болен. Этот смысл старого слоя НОЛИ тоже весьма подходил для нуля в позиционной системе. Ведь цифра ноль обозначает как бы не осуществившуюся возможность иметь значащую цифру в данном разряде.
Итак, название новой цифры НОЛЬ, позволившей ввести новую для своего времени позиционную систему счисления возникло, скорее всего, на основе именно русского языка. Так же как и новые обозначения «индо-арабских» цифр появились в результате легкого видоизменения старых русских цифр-букв. Все это происходило, как мы выяснили, не так уж давно — скорее всего, не ранее конца XVI века. А не в далеком Средневековье, как ошибочно утверждает скалигеровская хронология.
В заключение отметим, что в принципе можно пытаться искать буквы, похожие на «индо-арабские» цифры, и в других азбуках. Однако важно подчеркнуть, что для выяснения происхождения «индо-арабских» цифр подходит ДАЛЕКО НЕ ВСЯКАЯ АЗБУКА. Ведь требуется найти не просто какие-то буквы, «похожие на цифры» (что иногда удается), а буквы-цифры, ДЕЙСТВИТЕЛЬНО ИСПОЛЬЗОВАВШИЕСЯ В СРЕДНИЕ ВЕКА В КАЧЕСТВЕ ОБОЗНАЧЕНИЙ ЦИФР. Причем в силу естественной консервативности обозначений цифровые значения старых цифр-букв должны в основном сохраняться и в новой системе счисления. Как это имеет место для славянско-греческой азбуки и «индо-арабских цифр». Азбуки же, не использовавшиеся для обозначения цифр, привлекать не имеет смысла.
С нашим выводом о том, что ноль был изобретен только в конце XVI века, прекрасно согласуется и следующий известный исторический факт, поразительный с точки зрения скалигеровской хронологии. Напомним, что историки предлагают нам считать, что ноль был известен еще в глубокой древности. Однако в то же время известно, что математики даже в XVI веке ещё НЕ РАССМАТРИВАЛИ КОРНИ УРАВНЕНИЙ, РАВНЫЕ НУЛЮ [219], с. 153. Кроме того, как сообщают историки науки, естественная идея — оставить в правой части уравнения НОЛЬ, появилась лишь в конце XVI — начале XVII века [219], с. 153. Хотя, повторяем, ноль по мнению историков, был к тому времени якобы уже давным-давно известен. Цитируем: «Идея приравнивания уравнения нулю БЫЛА ЧУЖДА МАТЕМАТИКЕ ВОЗРОЖДЕНИЯ. ВПЕРВЫЕ КАНОНИЧЕСКУЮ ФОРМУ УРАВНЕНИЯ привел англичанин Т. Гэрриот (1580–1621) в книге „Применение аналитического искусства“» [219], с. 153.
Данный текст является ознакомительным фрагментом.