§ 11. Существуют ли в математике предрассудки?

§ 11. Существуют ли в математике предрассудки?

Математика считается точной и доказательной наукой, которая опирается на обоснованные определения и строгие доказательства. Поэтому ее теоремы считаются безусловно верными и не подлежащими сомнению. Предрассудкам (т. е. привычным, но ложным представлениям) в математике, конечно, не место. Однако проведем научное расследование.

Одной из важнейших теорем математики является теорема о непрерывной зависимости решений систем дифференциальных уравнений от их коэффициентов и параметров. Эта теорема лежит в основе всех инженерных расчетов. Действительно, если непрерывной зависимости решений от коэффициентов и параметров нет, то мы не можем быть уверены в том, что даже сколь угодно малые и поэтому неизбежные на практике отклонения действительных параметров рассчитываемого объекта от расчетных значений не приведут к коренным расхождениям между результатом расчета и реальностью, не можем быть уверены, например, в том, что здание, по расчету обязанное стоять долгие годы (как аквапарк «Трансвааль»), неожиданно не обрушится на головы посетителей. Поскольку данная теорема математиками считается доказанной, инженеры верят математикам и опираются на нее в своих расчетах как на незыблемую скалу.

Однако рассмотрим следующую систему двух дифференциальных уравнений

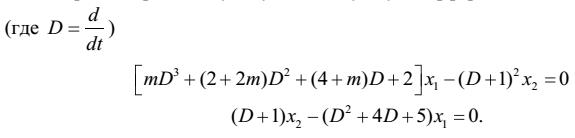                                                   (21)

Эта система, как уже говорилось в предыдущем разделе, описывает процессы в системе, состоящей из электропривода постоянного тока и регулятора с постоянными коэффициентами. Характеристический полином этой системы равен определителю (19), а мы уже убедились в параграфе 10, что в точке т = 1 характер корней характеристического полинома и характер решений системы резко меняются. Если т = 1 + є , где ? — малое число и ? < 0 , то в решении присутствуют только экспоненциально убывающие члены, если же малое в > 0, то в решении появляются стремительно растущие члены вида (20). Непрерывной зависимости решений от параметра т у системы (21) нет. При т = 1 эта зависимость терпит разрыв. Отметим, что подобных систем дифференциальных уравнений, не имеющих непрерывной зависимости решений от коэффициентов и параметров, довольно много. Примеры приведены в книге [2].

Из этих примеров следует, что одна из важнейших математических теорем не верна. Может ли такое быть? Многие математики заявляли — нет, такого быть не может! Теорема приводится во многих авторитетных учебниках, не могут все они ошибаться.

Да, теорема о непрерывной зависимости решений от параметров приведена — и причем с доказательством — во многих университетских учебниках. Примеры:

1. В учебнике для университетов: Степанов В. В. Курс дифференциальных уравнений. М., ГИТТЛ, 1953, 468 с., эта теорема рассмотрена на стр. 298—307.

2. В учебнике: Матвеев Н. М. Методы интегрирования обыкновенных дифференциальных уравнений. М., Высшая школа, 1967, 564 с., теорема рассмотрена на стр. 259—267.

3. В учебнике: Арнольд В. И. Обыкновенные дифференциальные уравнения. М., Наука, 1975, 239 с., теорема рассмотрена на стр. 186—204.

4. В учебнике: Матвеев Н. М. Обыкновенные дифференциальные уравнения, СПб., Специальная литература, 1996, 371 с., теорема рассмотрена на стр. 313—316.

Но — обратите особое внимание — во всех учебниках она доказана лишь для двух частных случаев: для системы из n уравнений первого порядка и для одного уравнения n -ого порядка. Для всех других многочисленных систем — как, например, для системы (21), которая состоит из уравнения третьего порядка для переменной X₁ и уравнения первого порядка для х₂ — теорема не доказана. Да, почти любую систему, состоящую из уравнений различных порядков, можно путем эквивалентных преобразований свести к системе из n уравнений первого порядка, для которой теорема доказана. Но для того, чтобы из этого вытекала верность теоремы для всех систем, необходимо доказать, что эквивалентные преобразования не меняют никаких свойств решений. А этого никто и никогда не доказывал (и не мог доказать — в книгах [1], [2] , [3] приводились все новые и новые примеры того, как эквивалентные преобразования меняли все новые и новые свойства решений — надо лишь внимательно исследовать; ищите и найдете).

Таким образом, мы убеждаемся, что одна из важнейших и известнейших математических теорем основана не на доказательстве, а на предрассудке — на привычном, но ложном убеждении большинства математиков в том, что эквивалентные преобразования якобы «ничего не меняют». Я опрашивал многих — и выпускников университетов, и их преподавателей: «как по-вашему — верна ли теорема о непрерывной зависимости для всех систем уравнений?» Все дружно отвечали: «да, верна. Верна потому, что для систем из n уравнений первого порядка в учебниках дано доказательство, а остальные системы приводятся к ним путем эквивалентных преобразований, которые «ничего не меняют»».

Мы убеждаемся, что предрассудки существуют и в математике, и предрассудки далеко не безобидные, поскольку они оказываются потом причиной многих техногенных катастроф с гибелью людей. И когда в книгах [1], [2], [3] опровергаются некоторые привычные положения и методики, то это не означает, что опровергаются какие-либо доказанные теоремы. Нет, они не опровергаются, а просто показывается необоснованность ставших привычными предрассудков. И в этом нет ничего страшного.

Наоборот, устранение предрассудков очень полезно для науки России для ее граждан, поскольку позволит избавиться от некоторых источников техногенных катастроф. Вероятность аварий и катастроф станет меньше.

А теперь идет самое интересное: посмотрите внимательно — как, каким образом формулируется теорема о непрерывной зависимости решений от параметров во всех перечисленных мною учебниках — от В. В. Степанова до В. И. Арнольда. Ни в одном из них не сказано: «теорема верна для всех систем уравнений, поскольку для систем из n уравнений первого порядка доказательство приведено, а остальные системы приводятся к ней эквивалентными преобразованиями». Это положение не высказано, оно «домысливается» преподавателями, а за ними — и студентами, слушающими лекции. Почему избран такой странный стиль изложения с необходимостью «домысливания»? Здесь можно высказать только догадку, или — как говорят «детективы» — версию. Вот эта версия: уважаемые авторы учебников понимали желательность дать доказательство этой важнейшей теоремы для всех систем — а не только состоящих из n уравнений первого порядка. Они пытались найти такое доказательство, но у них ничего не получилось. Теперь мы знаем, что получиться и не могло, поскольку в общем случае теорема (как показано в [2]) — не верна. Тогда они предпочли формулировку с необходимостью «домысливания», рассуждая (возможно) следующим образом: если теорема в дальнейшем будет доказана для всех систем, то «домысливание» окажется правильным и все будет в порядке. Если же теорема в общем виде будет опровергнута, то мы, авторы учебников, чисты: у нас сформулировано лишь верное утверждение о системах, состоящих из n уравнений первого порядка, а за «домысливание» мы не отвечаем.

Хотя это только «версия», но возможно, что так все и было (подробнее о данном вопросе — в [3] и в [12]).

Данный текст является ознакомительным фрагментом.